
The angle of minimum deviation for a prism is
Answer
501.3k+ views
Hint: The angle of minimum deviation is the minimum value of the angle of deviation when a ray of light passes through a prism. Substitute the value of angle of minimum deviation and angle of prism in the standard equation showing the relationship among angle of incidence, angle of minimum deviation, and the angle of prism.
Formula used:
Complete step by step answer:
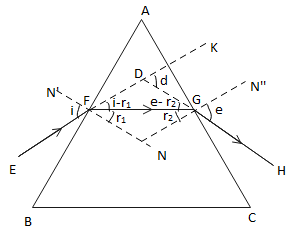
In the above figure, ABC represents the principle section of a glass prism having
Again, the ray FG is incident on the face AC at point G where
Now, if the prism was not there then the incident ray EF would have proceeded straight, but due to the presence of the prism it changes its path along the direction thereby making
Here we are dealing with the angle of minimum deviation which is the minimum value of angle of deviation when a ray of light passes through a prism. In minimum deviation position,
Again, for a prism
Using equation (i), we get
Also,
Given:
So, the correct answer is “Option C”.
Note: In case of minimum deviation through a prism following conditions are satisfied,
(i) The angle of incidence is equal to the angle of emergence.
(ii) The angle made by the ray, traveling through the material of the prism with, the normal to the two surfaces of the prism are equal to each other.
(iii) the ray passing through the material of the prism is parallel to its base.
Formula used:
Complete step by step answer:

In the above figure, ABC represents the principle section of a glass prism having
Again, the ray FG is incident on the face AC at point G where
Now, if the prism was not there then the incident ray EF would have proceeded straight, but due to the presence of the prism it changes its path along the direction thereby making
Here we are dealing with the angle of minimum deviation which is the minimum value of angle of deviation when a ray of light passes through a prism. In minimum deviation position,
Again, for a prism
Using equation (i), we get
Also,
Given:
So, the correct answer is “Option C”.
Note: In case of minimum deviation through a prism following conditions are satisfied,
(i) The angle of incidence is equal to the angle of emergence.
(ii) The angle made by the ray, traveling through the material of the prism with, the normal to the two surfaces of the prism are equal to each other.
(iii) the ray passing through the material of the prism is parallel to its base.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




