Question

The angle of rotational symmetry for a shape is $60{}^\circ $. What is the order of rotational symmetry?
[a] 6
[b] 4
[c] 3
[d] 8

Answer 1

Hint:Use the fact that if the angle of rotational symmetry is $\theta $, then the order of rotational symmetry is $\left[ \dfrac{360}{\theta } \right]$, where [x] denotes the greatest integer less or equal to x. Put $\theta =60$ and hence find the order of rotational symmetry of the shape.

Complete step-by-step answer:
Consider an object with the angle of rotational symmetry as x.
Hence, if we rotate the object by x degrees, the shape will remain unchanged.
Now, if we rotate the rotated image again by x degrees, again the net-shape will remain unchanged.
Hence if we rotate the original shape by 2x degrees, the shape will remain unchanged.
Continuing this way if we rotate the image by nx degrees, where n is a natural number, then the shape will remain unchanged.
Now, we know that the order of rotational symmetry of the shape is the number of times it can be rotated around a circle and still look the same.
Let the above shape be rotated n times and still look the same in a complete rotation.
Hence, we have
$nx\le 360 < \left( n+1 \right)x$
Dividing both sides by x, we get
$n\le \dfrac{360}{x} < n+1$
Hence, we have
$\left[ \dfrac{360}{x} \right]=n$(From the definition of the greatest integer function)
Hence, the order of the rotational symmetry, when the rotational angle of symmetry is $60{}^\circ $ is $\left[ \dfrac{360}{60} \right]=6$
Hence option [a] is correct.

Note: Verification:
A figure with a rotational angle of symmetry as 60 degrees is a regular hexagon.

Rotating clockwise by 60 degrees gives the following hexagon

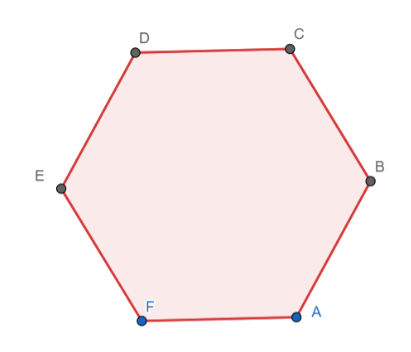
Clearly, the shape remains the same.
We can do the above process 4 more times till a complete rotation is achieved.
Hence the order of rotational symmetry is 6