Question

The angle of the sun above the horizon is 27.5 degrees. Find the approximate length of the shadow of a person who is 4.75 feet tall.
a)4.75 b.) 2.47 c.) 4.65 d.) 9.12 e.) 4.86

Answer 1

Hint:- Draw diagram to get a clear picture about what needs to be found. Use concept of trigonometry ratio, mostly we use
$\tan \theta = \frac{{\text{p}}}{{\text{b}}};$ p🡪perpendicular
               b🡪base

Complete step-by-step answer:
In this problem, we are given the length of a person and have to find the length of the shadow formed by the man, and the angle of the sun above the horizon is also given which is equal to ${27.5^\circ }$.
We can solve the above question by the trigonometric approach:
According to the question;

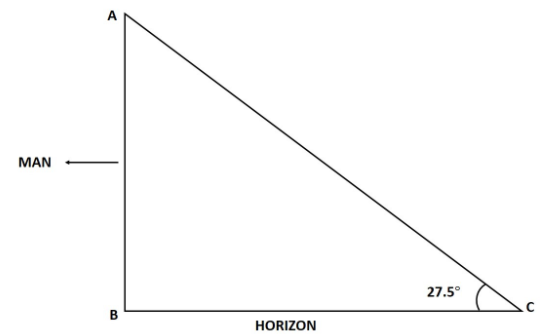
Here AB is the man, with the length of 4.75 feet long.
In this diagram, we have one of the angles given and the perpendicular side is also given. So, we will use the tangent angle concept;

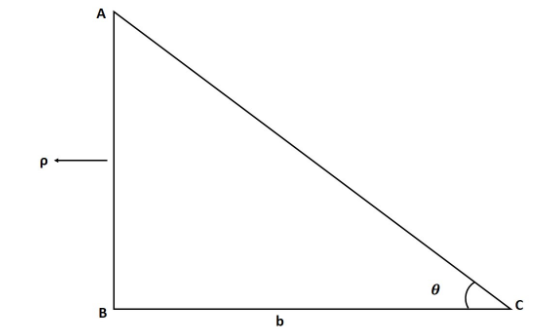
Here, $\tan \theta = \frac{{\text{p}}}{{\text{b}}}$
So, According to question;
Let BC = x;
$ \Rightarrow \tan \left( {{{27.5}^\circ }} \right) = \frac{{4.75}}{x}$
$ \Rightarrow x = \frac{{4.75}}{{\tan \left( {{{27.5}^\circ }} \right)}}$

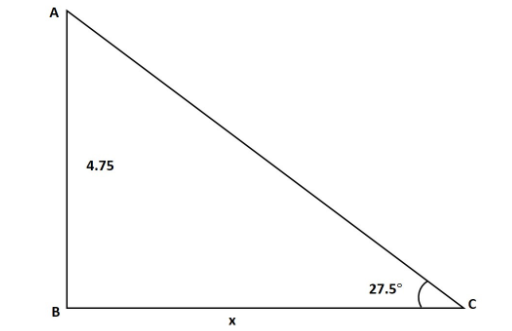
$ \Rightarrow x = \frac{{4.75}}{{0.52}}$ $\left[ {\therefore \tan \left( {{{27.5}^0}} \right) = 0.52} \right]$
$ \Rightarrow \boxed{x = 9.12}$
$\therefore $ approximate length of the shadow of a person who is 4.75 feet tall is $\boxed{9.12\;{\text{feet}}}$
Hence correct option is d.

Note:- Here we should remember value of tan$\left( {{{27.5}^\circ }} \right) = 0.52.$ In the similar way, the value of $\tan \left( {{{52}^\circ }} \right) = 1.27$ and so on.
Points to remember in solving height and distance problems:
1.Angle at which the observer views the topmost point of the object (angle of elevation).
2.The angle at which the observer views the object when the observer is on top of a tower/building (angle of depression)