Question

The angles of elevation and depression of the top and bottom of a lighthouse from the top of a 60 m high building are 30° and 60°, respectively. Find the difference between the heights of the lighthouse and building.

Answer 1

Hint – In order to find the difference between their heights, we consider all the given data and make a figure representing the lighthouse and the building. Both the lighthouse and the building are vertically perpendicular to the ground, therefore we can use the Tan function properties in a right angled triangle to find the answer.

Complete step-by-step answer:
Given data,
Height of the building = 60 m
Angle of elevation from the building to the top of lighthouse = 30°
Angle of depression from the building to the bottom of lighthouse = 60°

Now let us sketch a diagram which depicts all the data given in the question, it looks like -

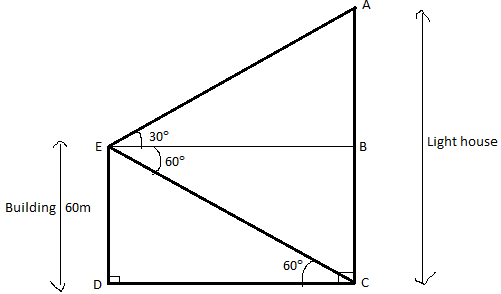
From the diagram, we get angle of elevation ∠AEB = 30° and angle of depression ∠BEC = 60°.
Both the lines ED and AC representing the building and the lighthouse respectively are parallel to each other because they are perpendicular to the ground. Therefore the angles ∠BEC and ∠ECD form alternate angles in between parallel lines.
According to the property of alternate angles, ∠BEC = ∠ECD.
⟹∠BEC = ∠ECD = 60°

Now let us consider the ∆ECD,
${\text{Tan 60}}^\circ {\text{ = }}\dfrac{{{\text{ED}}}}{{{\text{DC}}}}$
(From the figure ED = 60 m and from the trigonometric table of tan function, Tan 60° =$\sqrt 3 $)
$
   \Rightarrow {\text{Tan 60}}^\circ = \sqrt 3 {\text{ = }}\dfrac{{60}}{{{\text{DC}}}} \\
   \Rightarrow {\text{DC = 20}}\sqrt 3 {\text{ m - - - - }}\left( 1 \right) \\
$

Let us consider the ∆AEB,
${\text{Tan 30}}^\circ {\text{ = }}\dfrac{{{\text{AB}}}}{{{\text{EB}}}}$
(From the figure EB = DC =${\text{20}}\sqrt 3 {\text{ m}}$ and from the trigonometric table of tan function, Tan 30° =$\dfrac{1}{{\sqrt 3 }}$)
$
   \Rightarrow {\text{Tan 30}}^\circ {\text{ = }}\dfrac{1}{{\sqrt 3 }}{\text{ = }}\dfrac{{{\text{AB}}}}{{20\sqrt 3 }} \\
   \Rightarrow {\text{AB = }}\dfrac{{20\sqrt 3 }}{{\sqrt 3 }} \\
   \Rightarrow {\text{AB = 20m}} \\
$

The height of the building from the figure is ED and the height of the lighthouse is AC, the difference between their heights is AB, since ED = AC from the figure.
Therefore the difference between the heights of the building and the light house is AB = 20 m.

Note – In order to solve this type of question the key is to know the meaning of angle of elevation and the angle of depression. This is the main part of constructing an appropriate diagram in order to solve the question easily.
Angle of elevation is the angle from the horizontal upward to an object whereas the angle of depression is the angle from the horizontal downwards to an object.
Realizing that the building and the lighthouse form right angled triangles helps us apply the concept of trigonometric functions. Having knowledge in the trigonometric table of tan function is necessary.