Question

The angular amplitude of a simple pendulum is ${{\theta }_{\circ }}$. The maximum tension in its string will be
$\text{A}\text{. }mg(1-{{\theta }_{\circ }})$
$\text{B}\text{. }mg(1+{{\theta }_{\circ }})$
$\text{C}\text{. }mg(1-\theta _{\circ }^{2})$
$\text{D}\text{. }mg(1+\theta _{\circ }^{2})$

Answer 1

Hint: The maximum tension will be when $\theta =0$. Find the expression for the tension in the string when $\theta =0$. Forces on the bob of the pendulum, other than tension are gravitational force and centrifugal force ($\dfrac{m{{v}^{2}}}{l}$). Find the velocity of bob by using the work-energy theorem. Then find an expression of l in terms of ${{\theta }_{\circ }}$.

Complete step-by-step answer:
Suppose a pendulum is released from an angle of ${{\theta }_{\circ }}$. It will accelerate due to the force of gravity as shown in the figure.

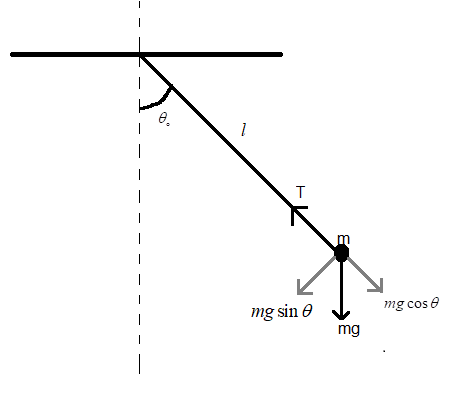
The tension in the string of the pendulum will balance the component of the gravitational force that is parallel to the string of the pendulum.
Suppose at some time t the string of the pendulum makes an angle $\theta $. Then the tension in the string will balance the parallel component of mg i.e. $mg\cos \theta $.
In addition to the force $mg\cos \theta $, there will one force that has to be balanced by the tension force in the string and that the centrifugal force, which is equal to $\dfrac{m{{v}^{2}}}{l}$,
where m is the mass of the bob, velocity of the bob and l is the length of the bob. This force is in the same direction of the force $mg\cos \theta $.
Therefore, the tension force (T) is equal to $T=mg\cos \theta +\dfrac{m{{v}^{2}}}{l}$ …….(i).
Let us find the velocity of the bob.
This can be found by the work-energy theorem. When the pendulum comes down, the force of gravity does a work, which is equal to the change in kinetic energy of the bob.
Suppose the bob has come down by a height of h. using the formula $\text{W = force }\!\!\times\!\!\text{ displacement perpendicular to force}$, work done on the bob will be equal to
$W=mgh$.
The change in kinetic energy of the bob will be $\dfrac{1}{2}m{{v}^{2}}$.
Therefore, $W=mgh=\dfrac{1}{2}m{{v}^{2}}$ .
$\Rightarrow {{v}^{2}}=2gh$. Substitute this value in equation (i).
$T=mg\cos \theta +\dfrac{m(2gh)}{l}$ …….(ii).
From the equation (ii) it is clear that T will be maximum when $\cos \theta $ and h is maximum.
The maximum value of $\cos \theta $ is when $\theta =0$ and when $\theta =0$, h is also maximum.
You may understand this better if you see the figure below.

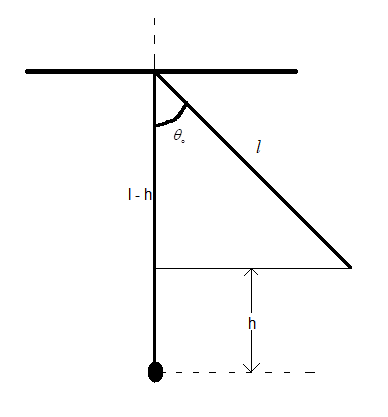
As you can see in the figure, $\cos {{\theta }_{\circ }}=\dfrac{l-h}{l}$.
$\Rightarrow h=l(1-\cos {{\theta }_{\circ }})$
Therefore, T is maximum when $\cos \theta =1$ and $h=l(1-\cos {{\theta }_{\circ }})$
Substitute these values in equation (ii).
$\Rightarrow T=mg+\dfrac{m(2gl(1-\cos {{\theta }_{\circ }}))}{l}$
$\Rightarrow T=mg+2mg(1-\cos {{\theta }_{\circ }})$ …….(iii).
Let assume that ${{\theta }_{\circ }}$ is a very small angle.
For small angles, $\cos \theta =1-\dfrac{{{\theta }^{2}}}{2}$
Therefore equation (iii) can be written as,
$\Rightarrow T=mg+2mg\left( 1-\left( 1-\dfrac{\theta _{\circ }^{2}}{2} \right) \right)$
$\Rightarrow T=mg+2mg\left( 1-1+\dfrac{\theta _{\circ }^{2}}{2} \right)$
$\Rightarrow T=mg+mg\theta _{\circ }^{2}=mg\left( 1+\theta _{\circ }^{2} \right)$
Hence, the correct option is D.

Note: When a particle is in a circular motion rotating about a fixed axis of rotation, it has two types of acceleration. One is along (parallel) the direction of its velocity called tangential acceleration (${{a}_{T}}$). This acceleration is due to the torque generated on the body. The magnitude of ${{a}_{T}}=r\alpha $, where r is the radius of the circle and $\alpha $ is the angular acceleration of the particle about the axis.
Other acceleration is due to the circular motion of the body, called centripetal acceleration (${{a}_{T}}$). Centripetal acceleration is perpendicular to the direction of the body’s velocity or along the direction of the radius. And ${{a}_{T}}=\dfrac{{{v}^{2}}}{r}$.