Question

The area of rectangle with 5cm length and 4cm as breadth as:
\[\begin{array}{l}(a){\rm{ 20c}}{{\rm{m}}^{\rm{2}}}\\{\rm{(b) 25c}}{{\rm{m}}^{\rm{2}}}\\{\rm{(c) 10c}}{{\rm{m}}^{\rm{2}}}\\{\rm{(d) 15c}}{{\rm{m}}^{\rm{2}}}\end{array}\]

Answer 1

Hint: We know that a rectangle is a quadrilateral having all angles are right angles. We will use the formula of area of rectangle having length l and breadth b is given by,
\[Area = l \times b{\rm{ sq}}{\rm{.units}}\]
We have been given the length and breadth of the rectangle in the question, so we can directly substitute them in the above formula and get the answer.

Complete step-by-step answer:
We have been asked to find the area of the rectangle with 5cm as length and 4cm as breadth. First of all, let us consider a rectangle, it is a quadrilateral having two sets of parallel sides of equal length and opposite to each other. All angles are right angles. So, let us draw a figure from the above details we have.

We will draw the rectangle and mark it as ABCD. The length is given as \[ = 5{\rm{cm}}\]and breadth\[ = {\rm{4cm}}\].

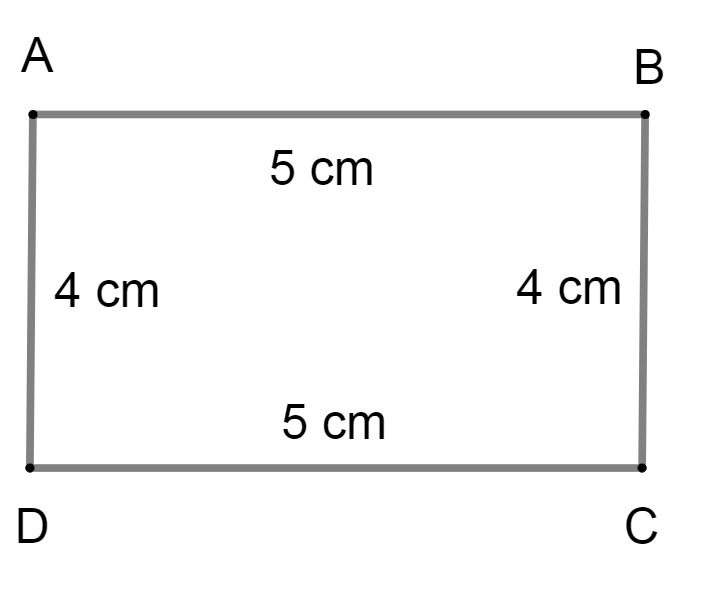
We know that area of a rectangle having length l and breadth b is given by,
\[Area = l \times b{\rm{ sq}}{\rm{.units}}.\]

Now, we will substitute the known values of l and b in it as shown below,

\[\begin{array}{l}Area = l \times b{\rm{ sq}}{\rm{.units}}.\\ \Rightarrow Area = \left( {5 \times 4} \right)c{m^2}\\ \Rightarrow 20c{m^2}\end{array}\]

Therefore, the correct option is (a).

Note: Remember the fact about a rectangle that is a plane two-dimensional figure having 4 sides of which two pairs of parallel sides and each interior angle equals \[{90^ \circ }\]. Also, a square is always a type of rectangle and a parallelogram and rhombus can only be rectangle when their interior angles are each \[{90^ \circ }\].
You can also calculate the area of the rectangle by joining a pair of its diagonal end points and making two triangles and the summation of the area of the triangles given the area of the rectangle. Let us consider the figure as below,

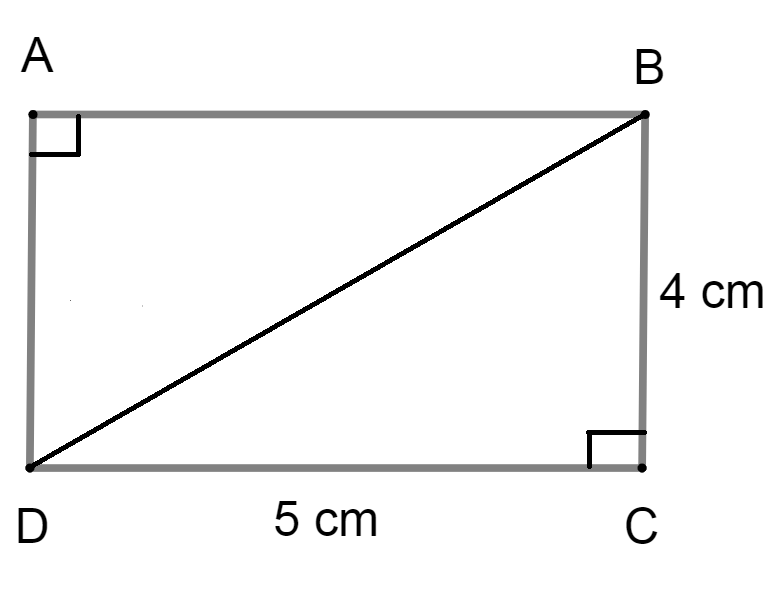
Now we have two equal right-angled triangles, ABD and BDC. The area of rectangle ABCD will be \[2 \times {\rm{ area\ of\ triangle BDC}}\].
Let us consider triangle BCD. Now we have the height as 4 cm and base as 5 cm. We know that the area of the triangle is \[\dfrac{1}{2} \times {\rm{base}} \times {\rm{height}}\].
So, we get area of triangle BDC as \[\dfrac{1}{2} \times 4 \times 5 = 10\,c{m^2}\]
Therefore, the area of the rectangle will be \[ = 2 \times 10 = 20c{m^2}\].