Question

The area of region bounded by the parabola ${{y}^{2}}=16{{x}^{2}}$ & its latus rectum is
A. $\dfrac{64}{3}sq\text{ unit}$
B. $\dfrac{128}{3}sq\text{ unit}$
C. $\dfrac{32}{3}sq\text{ unit}$
D. $\dfrac{16}{3}sq\text{ unit}$

Answer 1

Hint: Plot the parabola & draw the line of latus. Find the point of intersection and integrate the curve i.e. ${{y}^{2}}=16x$ i.e.$y=4\sqrt{x}$ .Limit values will be the values of x and since it's symmetric so we can double the area.

Complete step by step solution:
Compare the given parabola ${{y}^{2}}=16{{x}^{2}}$
with${{y}^{2}}=4ax$

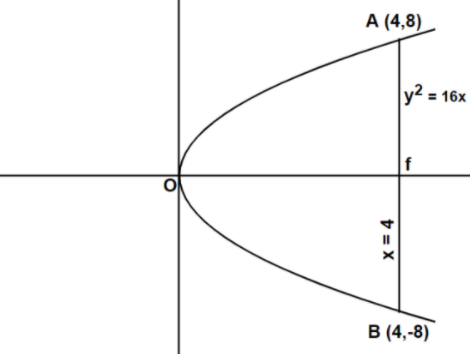
we get
$4a=16$
$\begin{align}
  & a=\dfrac{16}{4} \\
 & a=4 \\
\end{align}$
$\therefore $ Focus is F$\left( a,0 \right)$ i.e. F$\left( 4,0 \right)$
Equation of latus rectum
 For $x=a$
That is, $x=4$
For $x=4$,${{y}^{2}}=16x$
 $\begin{align}
  & \Rightarrow {{y}^{2}}=16\times 4=64 \\
 & \Rightarrow y=\pm 8 \\
 & \Rightarrow {{y}^{2}}=16x \\
 & \Rightarrow y=\sqrt{16x}=4\sqrt{4x} \\
\end{align}$
Now Area of OAFB$=2$Area of OAF
\[\begin{align}
  & =2\int\limits_{0}^{4}{ydx=2\int\limits_{0}^{4}{4\sqrt{x}}dx} \\
 & =8\int\limits_{0}^{4}{{{x}^{1/2}}dx} \\
 & =8\dfrac{{{x}^{3/2}}}{3/2}\underset{0}{\overset{4}{\mathop{|}}}\, \\
 & =8\times \dfrac{2}{3}{{x}^{3/2}}\underset{0}{\overset{4}{\mathop{|}}}\, \\
 & =16\left[ {{\left( 4 \right)}^{3/2}}-{{0}^{3/2}} \right] \\
 & =\dfrac{16}{3}\times 8=\dfrac{128}{3}sq\text{ units} \\
\end{align}\]

Additional information:

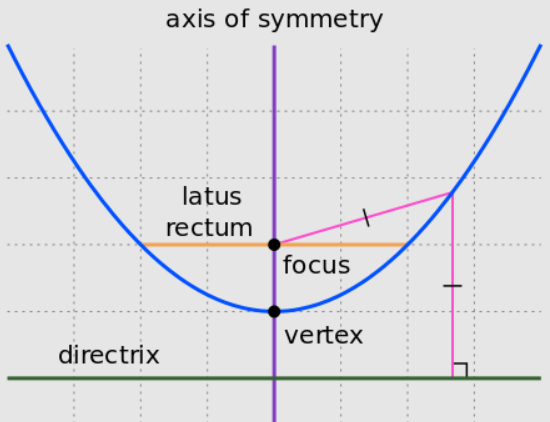
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped.
A parabola can also be defined geometrically as a set of points (locus of points) in the
A parabola is a set of points, such that for any point P of the set the distance |PF| to a fixed point F, the focus, is equal to the distance |Pl| to a fixed line l, the directrix $\{P:|PF|=|Pl|\}$
 For a parabola, the semi-latus rectum, p, is the distance of the focus from the directrix. Using the parameter p, the equation of the parabola can be rewritten as
${{x}^{2}}=2py$
In the case of f<0 the parabola has a downward opening.
The presumption that the axis is parallel to the y axis allows one to consider a parabola as the graph of a polynomial of degree 2, and conversely: the graph of an arbitrary polynomial of degree 2 is a parabola (see next section).
If one exchanges x and y, one obtains equations of the form${{y}^{2}}=2px$ . These parabolas open to the left (if p<0) or to the right (if p>0).

We can find the area of the region along the y-axis rather than x-axis. In that case function should be in terms of y & limits also for variable y.


Note: In symmetrical diagram or function if it is even function then the answer will be zero so to avoid that we must double the area. The knowledge about the parabola that is the equation of parabola which is ${{x}^{2}}=2py$, required to answer such questions. Whenever we are required to find the area under the given curve we always use integration.