Question

The area of the square built upon the hypotenuse of a right triangle is equal to the sum of the areas of the squares upon the remaining sides

Answer 1

Hint: Here we will use the relation inside the right-angled triangle, that relation is known as Pythagoras theorem.
If a, b, c are the sides of a right-angled triangle then \[{a^2} + {b^2} = {c^2}\] where c is the longest side know as hypotenuse
We will also use the concept that the area of the square with side is \[{a^2}\]

Complete step by step answer:
A right-angled triangle is given with sides a, b, c where c is the hypotenuse.
Our solution will be based on the below figure:

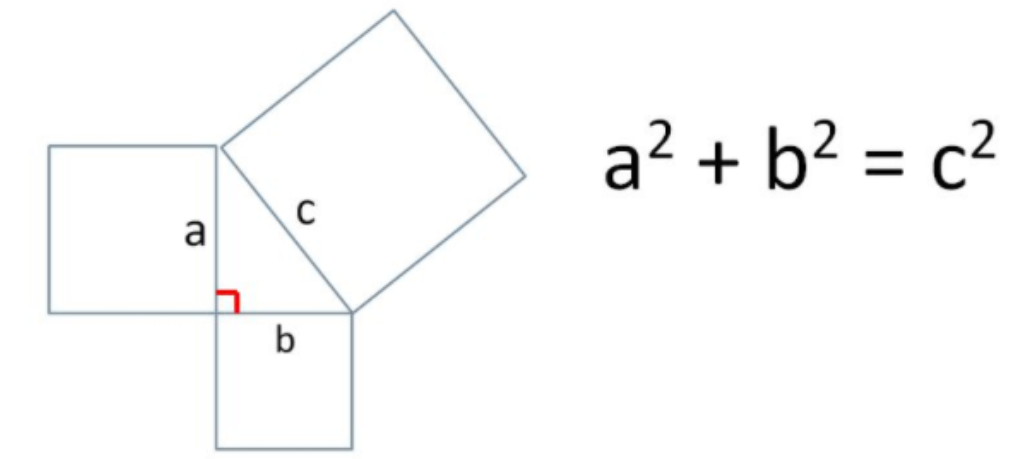
In the above figure the angle between side a and b is right and 90 degrees.
Squares are made on every side of the triangle
Here we can easily observe that area of the square whose side is a is equal to \[{a^2}\]
And we can also easily observe that area of the square whose side is b is equal to \[{b^2}\]
And we can also easily observe that area of the square whose side is c is equal to \[{c^2}\]
By Pythagoras theorem
\[{a^2} + {b^2} = {c^2}\]
(area of square with side a) + (area of square with side b) = (area of square with side c)

Hence, we can state that the given statement is True.

Note: In this type of questions we need to focus on the basic concept of geometry. We need to know the area of the square when the side of the square is given. Pythagora's theorem is need to be learnt.