
Answer
90k+ views
Hint: In this question, we need to find the area of the triangle formed by the line $x \cos \alpha + y \sin \alpha = p$ with the coordinate axes. First we need to find the value of $x$ and $y$ by substituting $x=0$ in the y axis then by substituting $y=0$ in the x axis. Then by using the area of the triangle, we can find the area of the triangle with the value of $x$ and $y$ . We can also use the trigonometric formulas in order to find the area.
Complete step by step solution:
Given $x \cos \alpha + y \sin \alpha = p$ which is the equation of the line.
Let $x$ and $y$ be the coordinate axes. Let O be the origin . The
Given the line$x \cos \alpha + y \sin \alpha = p$ meet the x axis and y axis at A and B respectively.
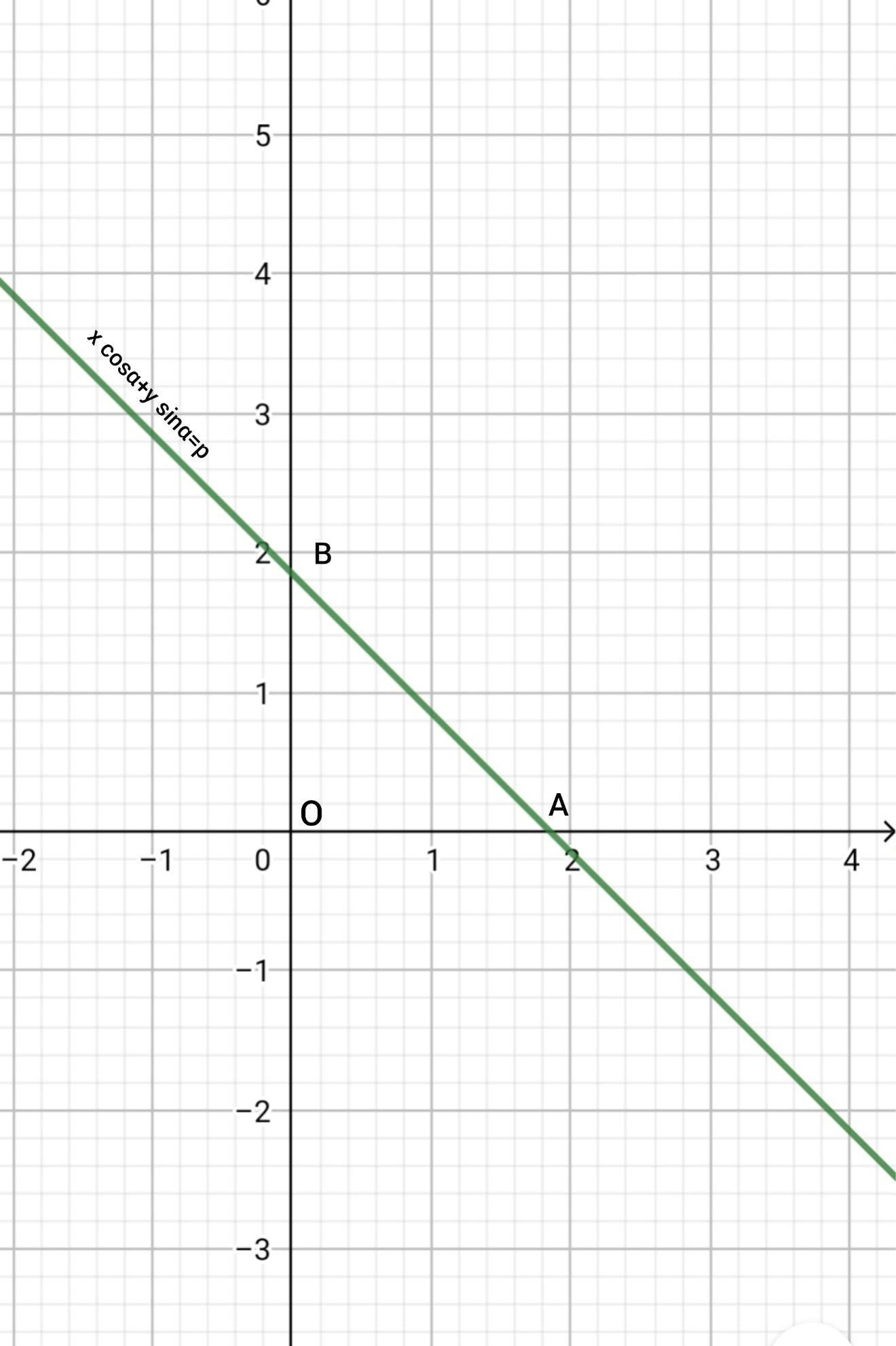
The given line is $x \cos \alpha + y \sin \alpha = p$
In x axis, $y = 0$
On substituting $y = 0$ in the given line,
We get,
$x \cos \alpha + (0) \times \sin \alpha = p$
On solving,
We get,
$x \cos \alpha = p$
On dividing both sides by $\cos \alpha $,
We get,
$x = \dfrac{p}{\cos \alpha}$
We can rewrite this as $x = p |\sec \alpha|$
Thus we get $OA = p |\sec\ \alpha|$
Now in y axis , $x = 0$
On substituting $x = 0$ in the given line,
We get,
$0 \times \cos \alpha + y \sin \alpha = p$
On solving,
We get,
$y \sin \alpha = p$
On dividing both sides by $\cos \alpha$,
We get,
$y = \dfrac{p}{\cos \alpha}$
We can rewrite this as $y = p |\text{cosec }\alpha|$
Thus we get $OB = p |\text{cosec }\alpha|$
Now area of the triangle OAB is
$\dfrac{1}{2} \times \left( OA \times OB \right)$
On substituting the value of OA and OB,
We get,
$A = \dfrac{1}{2} \times p \left| {\sec \alpha} \right| \times p \left|\text{cosec }\alpha \right|$
On solving,
We get,
$A = \dfrac{1}{2} \times \ p^{2}\left|\sec \alpha \times \text{cosec }\alpha \right|$
We can again rewrite this as,
$A = \dfrac{1}{2} \times \ p^{2}\left| \dfrac{1}{{\cos \alpha}} \times \dfrac{1}{{\sin \alpha}} \right|$
$A = \dfrac{1}{2} \times \ p^{2}\left| \dfrac{1}{{\cos \alpha \sin \alpha}} \right|$ ----- (1)
By using the trigonometric formula,
$\sin(A + B) = \sin A \cos B + \cos A\sin B$
Let us consider that $A = B = \alpha$
On substituting $\alpha$ in the place of $A$ and $B$,
We get
$\sin(\alpha + \alpha) = \sin \alpha \cos \alpha + \cos \alpha \sin \alpha$
On simplifying ,
We get,
$\sin(2\alpha) = 2\sin \alpha \cos \alpha$
On dividing both sides by $2$ ,
We get,
$\sin \alpha \cos \alpha = \dfrac{1}{2}\sin \left( 2\alpha \right)$
Now on substituting the value of ${\sin \alpha \cos \alpha}$ in equation (1) ,
We get,
$A = \dfrac{1}{2} \times \ p^{2}\left| \dfrac{1}{\dfrac{1}{2}\sin 2 \alpha} \right|$
On simplifying ,
We get
$A = p^{2}\left| \dfrac{1}{\sin 2\alpha} \right|$
We can rewrite this as $p^{2}\left| \text{cosec }2\alpha \right|$
Thus the area of the triangle formed by the line $x\cos \alpha + y\sin \alpha =p$ with the coordinate axes is $p^{2}\left|\text{cosec }\ 2\alpha \right|$
Option ‘D’ is correct
Note: In order to solve these questions , we should have a strong grip over areas of the triangle and trigonometric identities . We should keep in mind that we can directly find the area of the triangle by using the formula that the area of the triangle is half the product of base of the triangle and the height of the triangle.
Complete step by step solution:
Given $x \cos \alpha + y \sin \alpha = p$ which is the equation of the line.
Let $x$ and $y$ be the coordinate axes. Let O be the origin . The
Given the line$x \cos \alpha + y \sin \alpha = p$ meet the x axis and y axis at A and B respectively.

The given line is $x \cos \alpha + y \sin \alpha = p$
In x axis, $y = 0$
On substituting $y = 0$ in the given line,
We get,
$x \cos \alpha + (0) \times \sin \alpha = p$
On solving,
We get,
$x \cos \alpha = p$
On dividing both sides by $\cos \alpha $,
We get,
$x = \dfrac{p}{\cos \alpha}$
We can rewrite this as $x = p |\sec \alpha|$
Thus we get $OA = p |\sec\ \alpha|$
Now in y axis , $x = 0$
On substituting $x = 0$ in the given line,
We get,
$0 \times \cos \alpha + y \sin \alpha = p$
On solving,
We get,
$y \sin \alpha = p$
On dividing both sides by $\cos \alpha$,
We get,
$y = \dfrac{p}{\cos \alpha}$
We can rewrite this as $y = p |\text{cosec }\alpha|$
Thus we get $OB = p |\text{cosec }\alpha|$
Now area of the triangle OAB is
$\dfrac{1}{2} \times \left( OA \times OB \right)$
On substituting the value of OA and OB,
We get,
$A = \dfrac{1}{2} \times p \left| {\sec \alpha} \right| \times p \left|\text{cosec }\alpha \right|$
On solving,
We get,
$A = \dfrac{1}{2} \times \ p^{2}\left|\sec \alpha \times \text{cosec }\alpha \right|$
We can again rewrite this as,
$A = \dfrac{1}{2} \times \ p^{2}\left| \dfrac{1}{{\cos \alpha}} \times \dfrac{1}{{\sin \alpha}} \right|$
$A = \dfrac{1}{2} \times \ p^{2}\left| \dfrac{1}{{\cos \alpha \sin \alpha}} \right|$ ----- (1)
By using the trigonometric formula,
$\sin(A + B) = \sin A \cos B + \cos A\sin B$
Let us consider that $A = B = \alpha$
On substituting $\alpha$ in the place of $A$ and $B$,
We get
$\sin(\alpha + \alpha) = \sin \alpha \cos \alpha + \cos \alpha \sin \alpha$
On simplifying ,
We get,
$\sin(2\alpha) = 2\sin \alpha \cos \alpha$
On dividing both sides by $2$ ,
We get,
$\sin \alpha \cos \alpha = \dfrac{1}{2}\sin \left( 2\alpha \right)$
Now on substituting the value of ${\sin \alpha \cos \alpha}$ in equation (1) ,
We get,
$A = \dfrac{1}{2} \times \ p^{2}\left| \dfrac{1}{\dfrac{1}{2}\sin 2 \alpha} \right|$
On simplifying ,
We get
$A = p^{2}\left| \dfrac{1}{\sin 2\alpha} \right|$
We can rewrite this as $p^{2}\left| \text{cosec }2\alpha \right|$
Thus the area of the triangle formed by the line $x\cos \alpha + y\sin \alpha =p$ with the coordinate axes is $p^{2}\left|\text{cosec }\ 2\alpha \right|$
Option ‘D’ is correct
Note: In order to solve these questions , we should have a strong grip over areas of the triangle and trigonometric identities . We should keep in mind that we can directly find the area of the triangle by using the formula that the area of the triangle is half the product of base of the triangle and the height of the triangle.
Recently Updated Pages
Name the scale on which the destructive energy of an class 11 physics JEE_Main

Write an article on the need and importance of sports class 10 english JEE_Main

Choose the exact meaning of the given idiomphrase The class 9 english JEE_Main

Choose the one which best expresses the meaning of class 9 english JEE_Main

What does a hydrometer consist of A A cylindrical stem class 9 physics JEE_Main

A motorcyclist of mass m is to negotiate a curve of class 9 physics JEE_Main



