
The area under velocity-time graph gives:
A. Acceleration
B. Distance
C. Displacement
D. velocity
Answer
507.3k+ views
3 likes
Hint – You can start by describing the velocity-time graph. Draw a general graph as an example. Find out the area of the velocity-time. Then use the relation between velocity, time and displacement
Complete step-by-step answer:
Equations are useful for explaining idealized scenarios, but they don't always cut it. In many instances it is much more efficient to use an image to describe the situation. Graphs can be considered as a mathematical picture and describe real world events in a compact form. Graphs of motion are available for several types of situations based on which of the kinematic quantities (time, position, velocity, acceleration) are assigned to the X axis and the Y axis.
An example of a graph of velocity with respect to time is shown below.
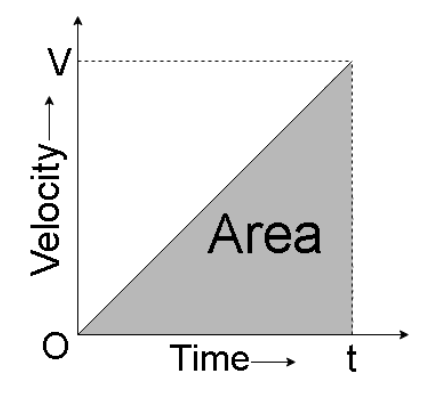
Here the velocity is plotted on X axis and time on the Y axis.
In the example we see that the area formed by the graph is in the shape of a right angles triangle, and we know for a right angled triangle
We also know that the relation of displacement, time and velocity are
Integrating both the sides, we get
If we compare equation 1 and equation 2, we see that the area of the velocity-time graph represents the displacement of an object in that time frame.
In the example we used, the area is in the shape of a right angled triangle but whatever the shape of the area of the velocity-time graph, it is always equal to the displacement.
Note: The velocity-time graph is a very useful graph. You can find out the displacement of an object by calculating the area of the graph, additionally you can also find the average or instantaneous acceleration of the body, by using the following relations
Complete step-by-step answer:
Equations are useful for explaining idealized scenarios, but they don't always cut it. In many instances it is much more efficient to use an image to describe the situation. Graphs can be considered as a mathematical picture and describe real world events in a compact form. Graphs of motion are available for several types of situations based on which of the kinematic quantities (time, position, velocity, acceleration) are assigned to the X axis and the Y axis.
An example of a graph of velocity with respect to time is shown below.

Here the velocity is plotted on X axis and time on the Y axis.
In the example we see that the area formed by the graph is in the shape of a right angles triangle, and we know for a right angled triangle
We also know that the relation of displacement, time and velocity are
Integrating both the sides, we get
If we compare equation 1 and equation 2, we see that the area of the velocity-time graph represents the displacement of an object in that time frame.
In the example we used, the area is in the shape of a right angled triangle but whatever the shape of the area of the velocity-time graph, it is always equal to the displacement.
Note: The velocity-time graph is a very useful graph. You can find out the displacement of an object by calculating the area of the graph, additionally you can also find the average or instantaneous acceleration of the body, by using the following relations
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




