
The areal velocity of an object of mass m=2kg revolving around another object is given by
A.
B.
C.
D.
Answer
492.9k+ views
Hint: We could assume that the body is revolving around the other object in a circular path. We know that the areal velocity is the rate at which the area is swept by the revolving body, so, we could substitute the circle’s area and time taken for one complete revolution around the circumference of a circle in the expression for areal velocity. We also know the expression for angular momentum, so, we could find the relationship between angular momentum and areal velocity from the known expressions and hence find the answer.
Formula used:
Expression for areal velocity,
Areal velocity=
Expression for angular momentum,
Complete step-by-step answer:
We are given a body of mass m=2kg that is revolving around another body. Let us assume that the body of mass m revolves around the other body in a circular path. This can be represented by,
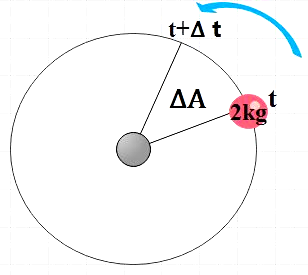
In the above given figure, at time t the body is located at a certain point and moves to another point in the interval of ∆t. The area swept by the body during that small time interval is ∆A. We are also given the areal velocity of the body of mass m. We know that areal velocity is defined as the rate at which the body sweeps out the area as it moves along a curve. That is, areal velocity is given by the expression,
Areal velocity=
A is the total area covered at the end of one complete revolution of the body of mass m around the other object, which in the above case is the area of a circle. Therefore, total area swept in time t is given by,
Time taken for one revolution is given by,
Where, 2πr is the circumference of the circle.
Substituting (2) and (3) in (1), we get,
Areal velocity=
We know that the angular momentum for a mass m is given by,
Substituting (5) in equation (4), we get the areal velocity as,
In the question, we are given the following values,
Substituting these values in equation (6), we get the angular momentum as,
Therefore, the angular momentum of the particle is
So, the correct answer is “Option B”.
Note: Even if we had not assumed that the path of revolution of the body was circular, we would have got the same result for the expression between angular momentum and areal velocity.
In the above diagram vector area swept by the body is given by (infinitely small area ∆A of a circle can be considered a triangle),
But angular momentum,
From (a) and (b),
This is the same expression as we got under our assumption.
Formula used:
Expression for areal velocity,
Areal velocity=
Expression for angular momentum,
Complete step-by-step answer:
We are given a body of mass m=2kg that is revolving around another body. Let us assume that the body of mass m revolves around the other body in a circular path. This can be represented by,

In the above given figure, at time t the body is located at a certain point and moves to another point in the interval of ∆t. The area swept by the body during that small time interval is ∆A. We are also given the areal velocity of the body of mass m. We know that areal velocity is defined as the rate at which the body sweeps out the area as it moves along a curve. That is, areal velocity is given by the expression,
Areal velocity=
A is the total area covered at the end of one complete revolution of the body of mass m around the other object, which in the above case is the area of a circle. Therefore, total area swept in time t is given by,
Time taken for one revolution is given by,
Where, 2πr is the circumference of the circle.
Substituting (2) and (3) in (1), we get,
Areal velocity=
We know that the angular momentum for a mass m is given by,
Substituting (5) in equation (4), we get the areal velocity as,
In the question, we are given the following values,
Substituting these values in equation (6), we get the angular momentum as,
Therefore, the angular momentum of the particle is
So, the correct answer is “Option B”.
Note: Even if we had not assumed that the path of revolution of the body was circular, we would have got the same result for the expression between angular momentum and areal velocity.
In the above diagram vector area swept by the body is given by (infinitely small area ∆A of a circle can be considered a triangle),
But angular momentum,
From (a) and (b),
This is the same expression as we got under our assumption.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




