Question

The axis of a parabola is along the line $y=x$ and the distance of the origin from its vertex is $\sqrt{2}$ and that from its focus is $2\sqrt{2}$ respectively. If the vertex and focus both lie in the first quadrant then the equation of the parabola is
(a) ${{\left( x+y \right)}^{2}}=\left( x-y-2 \right)$
(b) ${{\left( x-y \right)}^{2}}=\left( x+y-2 \right)$
(c) ${{\left( x-y \right)}^{2}}=4\left( x+y-2 \right)$
(d) ${{\left( x-y \right)}^{2}}=8\left( x+y-2 \right)$

Answer 1

Hint: First, we have to find vertex point and focus point by drawing graphs and plotting all the given values. Then by using Pythagoras formula we can find both the points i.e. vertex and focus. Then we will find the directrix of line $y=x$ which will be perpendicular to it i.e. line $y=-x$ . After this we should know that the distance from the directrix to the point on parabola is equal to point from parabola to the focus point. So, using this we will find distance using formula $\sqrt{{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}}$ for finding distance of parabola to focus and $\left| \dfrac{x+y}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$ for finding perpendicular distance from directrix from parabola. Thus, we will get the answer.

Complete step-by-step answer:
First, we will draw a graph in the cartesian plane of line $y=x$ which means that it will be passing directly from the centre in the first quadrant and plotting the vertex and focus point on the line $y=x$ . So, we will get as

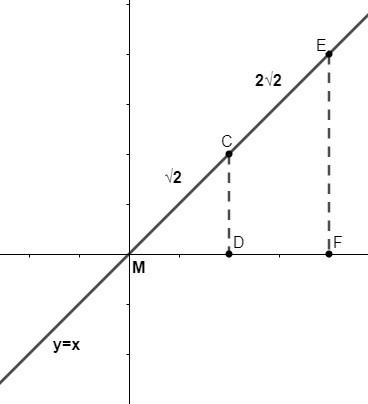
Now, here distance of vertex from origin i.e. $CM=\sqrt{2}$ and of focus from origin is $ME=2\sqrt{2}$ which will be equal to $CM+CE=2\sqrt{2}$ .
Here, the directrix will always be perpendicular to the line so that $MC=CE=\sqrt{2}$ . Therefore, the directrix of line $y=x$ will be $y=-x$ .
Now, if we see triangle CDM which is right angle triangle, value of sides CD and MD can be find out using Pythagoras theorem given as $C{{D}^{2}}+D{{M}^{2}}={{\left( \sqrt{2} \right)}^{2}}$.
So, we can come to know that ${{1}^{2}}+{{1}^{2}}={{\left( \sqrt{2} \right)}^{2}}=2$
So, the vertex point is $C\left( 1,1 \right)$ . …………………….(1)
Similarly, focus point E can be find out using Pythagoras theorem i.e. $E{{F}^{2}}+F{{M}^{2}}={{\left( 2\sqrt{2} \right)}^{2}}$
$E{{F}^{2}}+F{{M}^{2}}=8$
$\Rightarrow 4+4=8$ So, EF and FM will be 2, 2. Thus, focus point E will be $E\left( 2,2 \right)$.
Now, drawing the graph we will get as

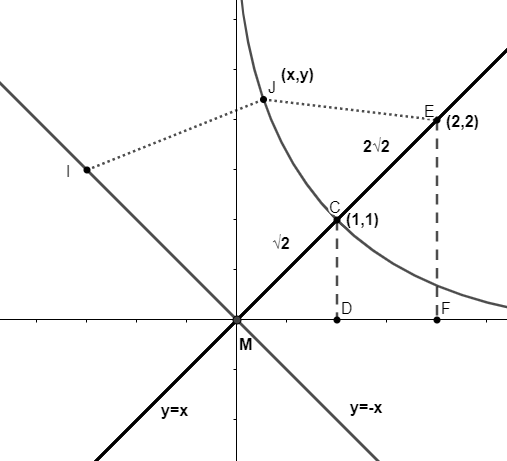
Here, we have drawn parabola passing through vertex point C. Also, we should know that distance from directrix to point on parabola is the same as point from parabola to the focus point.
Therefore, $IJ=JE$ so, we will find the distance by distance formula where I is the directrix $y=-x$ i.e. $x+y=0$ . So, using the formula $\sqrt{{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}}$ we get
 $IJ=JE$
$\Rightarrow \left| \dfrac{x+y}{\sqrt{{{1}^{2}}+{{1}^{2}}}} \right|=\sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}}$
where for IJ perpendicular distance formula is used i.e. $\left| \dfrac{x+y}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right|$, a and b are co-efficient of x and y.
So, now squaring on both the sides, and solving we get the equation as
\[\Rightarrow {{\left| \dfrac{x+y}{\sqrt{2}} \right|}^{2}}={{\left( \sqrt{{{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}} \right)}^{2}}\]
\[\Rightarrow \dfrac{{{\left( x+y \right)}^{2}}}{2}={{\left( x-2 \right)}^{2}}+{{\left( y-2 \right)}^{2}}\]
Now, on expanding the terms we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+2xy=2\left( {{x}^{2}}-4x+4 \right)+2\left( {{y}^{2}}-4y+4 \right)\]
Multiplying 2 inside the bracket, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+2xy=2{{x}^{2}}-8x+8+2{{y}^{2}}-8y+8\]
On re-arranging terms, we get
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-2xy=8x+8y-16\]
Here using the formula \[{{\left( x-y \right)}^{2}}={{x}^{2}}+{{y}^{2}}-2xy\] and taking 8 common from RHS, we get
\[\Rightarrow {{\left( x-y \right)}^{2}}=8\left( x+y-2 \right)\]
Thus, the equation of parabola is \[{{\left( x-y \right)}^{2}}=8\left( x+y-2 \right)\] .
Hence, option (d) is correct.

Note: Remember that in this type of problem drawing a figure is necessary by which we will come to know exactly what we have to find out. Also, do not forget to find the directrix line which is always perpendicular to the line given to us. Students sometimes try to put the value of focus point and vertex point in the option and see whether LHS is equal to RHS but that will not happen. So, please have a clear concept regarding the directrix part to avoid the mistakes.