Question

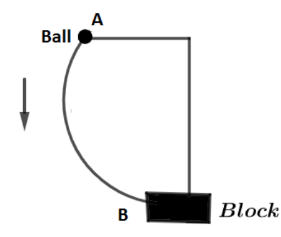
The ball is released when the string is horizontal. The collision between the ball and block is head on elastic. Find out velocities of the ball and the block immediately after the collision.

A. $ - \dfrac{1}{3}\sqrt {2gL} ,\dfrac{2}{3}\sqrt {2gL} $
B. $ - \dfrac{2}{3}\sqrt {2gL} ,\dfrac{{ - 1}}{3}\sqrt {2gL} $
C. $ - \dfrac{1}{9}\sqrt {2gL} , - \dfrac{2}{3}\sqrt {2gL} $
D. None of these

Answer 1

Hint:In order to solve this equation, we will use the principle of conservation of energy which states that “the total energy of a body is remains constant at any point of the motion of a body such that $K.E + P.E = $ constant” and an elastic collision is one in which linear momentum of a system remain conserved which means total initial momentum of a system before collision is equals to total final momentum of a system after collision. Total kinetic energy of a system is also conserved such that total kinetic energy before the collision is equal to the total final kinetic energy of the system after the collision.

Formula used:
Linear momentum of a body is given by $p = mv$ and Kinetic energy is given by $K.E = \dfrac{1}{2}m{v^2}$ where, $m$ is the mass of a body and $v$ is the velocity of a body. Potential energy of a body is $P.E = mgh$ where $g$ the acceleration due to gravity is and $h$ is the height up to which the body is moved against the gravity.

Complete step by step answer:
Now, when the ball is just released it has a potential energy of $P.E = mgL$ since, $L$ is the height between point $A$ and $B$. when ball just hit the block, let its velocity be ${u_1}$ and at point B it will have a kinetic energy of $K.E = \dfrac{1}{2}m{u_1}^2$ so, according to the conservation of energy,
${(P.E)_A} = {(K.E)_B}$
So,
$mgL = \dfrac{1}{2}m{u_1}^2$
$\Rightarrow {u_1} = \sqrt {2gL} \\ $
Now, just before the head on collision, the initial velocity of ball is ${u_1} = \sqrt {2gL} $ and initial velocity of block which is at rest is ${u_2} = 0$ and let the final velocities of ball and the black is ${v_1}$ and ${v_2}$ . Then using conservation of linear momentum with the diagram of collision is shown as:

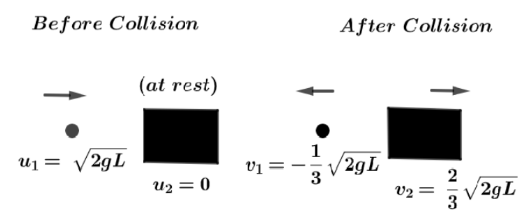
Initial momentum of system $ = $ Final momentum of system
$m{u_1} + 2m{u_2} = m{v_1} + 2m{v_2}$
$\Rightarrow m\sqrt {2gL} + 0 = m{v_1} + 2m{v_2}$
$\Rightarrow {v_1} + 2{v_2} = \sqrt {2gL} \to (i) \\ $
Now, it’s given that the collision is head on elastic. A head on elastic collision is one in which the velocity of approach is equal to the velocity of separation between two bodies.
Velocity of approach is ${u_1} - {u_2} = \sqrt {2gL} $
Velocity of separation is ${v_2} - {v_1}$ so,
Velocity of approach is $ = $ velocity of separation
${u_1} - {u_2} = {v_2} - {v_1}$
$\Rightarrow {v_2} - {v_1} = \sqrt {2gL} \to (ii) \\ $
Now, Adding equation $(i)and(ii)$ we get,
${v_1} + 3{v_2} - {v_1} = 2\sqrt {2gL} $
$\Rightarrow 3{v_2} = 2\sqrt {2gL} $
$\Rightarrow {v_2} = \dfrac{2}{3}\sqrt {2gL} $
Now, put this value of ${v_2} = \dfrac{2}{3}\sqrt {2gL} $ in equation ${v_1} + 2{v_2} = \sqrt {2gL} \to (i)$ we get,
${v_1} + \dfrac{4}{3}\sqrt {2gL} = \sqrt {2gL} $
$\Rightarrow {v_1} = - \dfrac{1}{3}\sqrt {2gL} $
So, the final velocity of ball is ${v_1} = - \dfrac{1}{3}\sqrt {2gL} $ and velocity of block is $\therefore {v_2} = \dfrac{2}{3}\sqrt {2gL} $

Hence, the correct option is A.

Note: It should be remembered that, when ball just came to collide the block its whole potential energy will convert into kinetic energy and the negative sign of the final velocity of the ball which is ${v_1} = - \dfrac{1}{3}\sqrt {2gL} $ indicates that ball will move in left direction after the collision which is an example of head-on collision in which the colliding body after the collision moves in opposite direction to the one in which its collides with another body.