Question

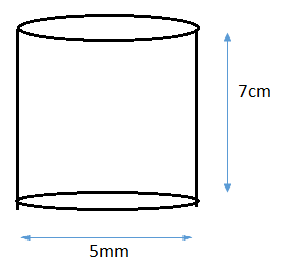
The barrel of a fountain pen, cylindrical in shape is 7cm long and 5mm in diameter. A full barrel of ink in the pen will be used upon writing 330 words on an average. How many words would use up a bottle of ink containing one fifth of a litre?

Answer 1

Hint: First calculate volume of cylinder given, now convert this volume into litres. So, this many litres are used for a given number of words, use cross multiplication method to calculate one fifth litre ink can be used for how many words. This will be your required result.

Complete step-by-step answer:
Given dimensions of the cylinder in the question:
Height = 7cm …………………(1)
Diameter = 5mm…………….(2)
By dividing with 2 on both sides of equation (2) we get
$\dfrac{\text{diameter}}{2}=\dfrac{5}{2}=2.5$

By using radius is half of the diameter, we can say radius = 2.5mm.
We know that the relation of mm, cm given by:
$100mm=10cm\Rightarrow 1mm=\dfrac{1}{10}cm$
By substituting this into radius, we get it as:
$\text{radius}=2.5\times \dfrac{1}{10}cm$
By simplifying the radius, we can say its value to be radius = 0.25cm
We know volume of a cylinder V, is given by formula
$V=\pi {{r}^{2}}h$
By substituting the values, we can write it in the form
$V=\pi \times {{\left( 0.25 \right)}^{2}}\times \left( 7 \right)$
By substituting value of $\pi \to \dfrac{22}{7}$ , we can write it in form of
$\text{Volume}=\dfrac{22}{7}\times {{\left( 0.25 \right)}^{2}}\times 7$
By cancelling the common terms, we can write it as
$\text{Volume=1}\text{.375c}{{\text{m}}^{3}}$
By relation between cubic centimetre, millilitre we get
$1c{{m}^{3}}=1ml$
By substituting that, we get volume of ink in total
Volume = 1.375 ml .
Given the value of ink present is written as $\dfrac{1}{5}lts.$ We know the relation as 1L = 1000ml. So, volume of ink $=\dfrac{1000}{5}=200ml$ . We have that 1.375ml ink gives 330 words, then 200ml gives how much. By cross multiplication, method we get
$\text{Number of words}=\dfrac{200\times 330}{1.375}\text{ }$
By simplifying we get it in form of below
$\text{Number of words}=200\times 240$
By calculating we get number of words written as
Number of words = 48000
So, with one fifth litre we can write 48000 words.

Note: Do the unit conversion properly as it is the only method followed by the cross multiplication method must be done properly because it is the base for the result we obtained. Alternate method is instead of converting the volume of the cylinder into litres you can convert the given volume of litres into cubic centimetres. Anyways you get the same result.