
The base angles of an isosceles triangle is 50 degrees. The size of vertical angle is:
A.
B.
C.
D.
Answer
492k+ views
1 likes
Hint: In this question, we need to determine the value of the vertical angle of the isosceles triangle such that the base angles of the triangle has been given as 55 degrees. For this, we will follow the property of the isosceles triangle along with the properties of the general triangles.
Complete step-by-step answer:
According to the question, the base angles of the isosceles triangle are
Let the value of the vertical angle of the isosceles triangle be
The following figure depicts the pictorial data given in the question
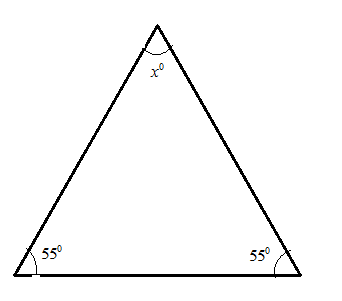
Following the property of the isosceles triangles which states that the two sides of the isosceles triangles are same and so the opposite angles associated with those sides will be equal and the vice-versa is also true.
Also, the sum of the interior angles of the triangles will be equal to 180 degrees. Mathematically,
Here, in the question the two interior angles of the isosceles triangle are 55 degrees each. So, substituting the values in the equation
Hence, the vertical angle of the isosceles triangle is 70 degrees.
So, the correct answer is “Option C”.
Note: In an isosceles triangle, the vertical angle is the angle other than the two equal angles (also known as the base angles). Two of the angles of the isosceles triangles are always equal.
Complete step-by-step answer:
According to the question, the base angles of the isosceles triangle are
Let the value of the vertical angle of the isosceles triangle be
The following figure depicts the pictorial data given in the question

Following the property of the isosceles triangles which states that the two sides of the isosceles triangles are same and so the opposite angles associated with those sides will be equal and the vice-versa is also true.
Also, the sum of the interior angles of the triangles will be equal to 180 degrees. Mathematically,
Here, in the question the two interior angles of the isosceles triangle are 55 degrees each. So, substituting the values in the equation
Hence, the vertical angle of the isosceles triangle is 70 degrees.
So, the correct answer is “Option C”.
Note: In an isosceles triangle, the vertical angle is the angle other than the two equal angles (also known as the base angles). Two of the angles of the isosceles triangles are always equal.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

List some examples of Rabi and Kharif crops class 8 biology CBSE

How many ounces are in 500 mL class 8 maths CBSE

What is the feminine gender of a stag class 8 english CBSE

Give me the opposite gender of Duck class 8 english CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE




