
The base of a prism is triangular in shape with sides 3 cm., 4 cm. and 5 cm. Find the volume of the prism if its height is 10 cm.
Answer
495.9k+ views
Hint: We first find the area
Complete step-by-step solution:
We know that a prism is a three-dimensional object polyhedron with
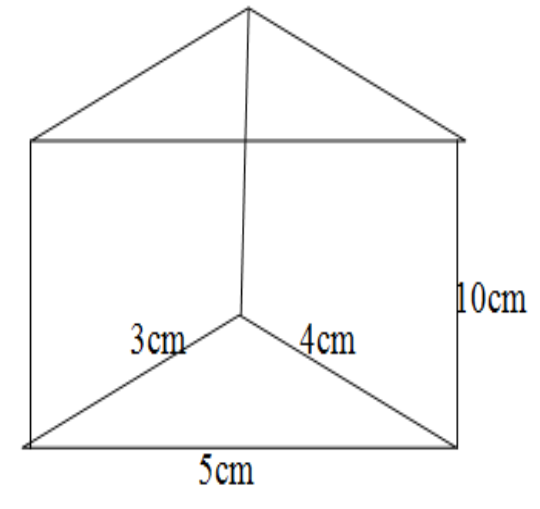
If the base of the prism is a triangle then it is a polyhedron with the base as at the bottom and the top as a 3-sided triangle and 3 parallelogram-shaped faces joining both the bases. We are given in the question that the base is triangular and the sides of the triangle at the base are of length 3cm, 4c, 5cm. The height is given as
We know that the area of any triangle with length of the sides
Now we can find the volume of the prism as
So the volume of the triangle is obtained as 60 cubic cm.
Note: We can alternatively calculate the area of the triangle at the base by observing the triangle is right-angled. The triplet length of sides
Complete step-by-step solution:
We know that a prism is a three-dimensional object polyhedron with

If the base of the prism is a triangle then it is a polyhedron with the base as at the bottom and the top as a 3-sided triangle and 3 parallelogram-shaped faces joining both the bases. We are given in the question that the base is triangular and the sides of the triangle at the base are of length 3cm, 4c, 5cm. The height is given as
We know that the area of any triangle with length of the sides
Now we can find the volume of the prism as
So the volume of the triangle is obtained as 60 cubic cm.
Note: We can alternatively calculate the area of the triangle at the base by observing the triangle is right-angled. The triplet length of sides
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Chandigarh is the capital of A Punjab B Haryana C Punjab class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE




