Question

The base of a right pyramid is an equilateral triangle, each side of which is $6\sqrt{3}\,cm$ long and its height is 4cm. Find the total surface area of the pyramid in $c{{m}^{2}}$.
\[\begin{align}
  & (a)\,\,64\sqrt{3} \\
 & (b)\,\,68\sqrt{3} \\
 & (c)\,\,72\sqrt{3} \\
 & (d)\,\,76\sqrt{3} \\
\end{align}\]

Answer 1

Hint: To solve the question above, we will find out what is a pyramid first. Then, we will look at the definition of the equilateral triangle. Now, to find the total surface area of the pyramid, we will first find the area of the equilateral triangle, we will find its height and apply the formula \[Area\,=\,\dfrac{b\times h}{2}\] Then, with the help of Pythagoras theorem, we will find the lateral edges of the pyramid. Then, with the help of formula \[Area\,=\,\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}\] we will find the area of lateral surface. Then, we will add all the areas to get the total area.

Complete step-by-step solution:
Before we solve the question, we must know what a pyramid is. A pyramid is a polyhedron that has a base, which is any polygon, and three or more triangular faces (also called lateral faces) that meet at a point called the apex.
An equilateral triangle is a triangle whose all sides are equal in length and each interior angle is ${{60}^{\circ }}$. So, now we will draw a triangular pyramid to understand the question better.

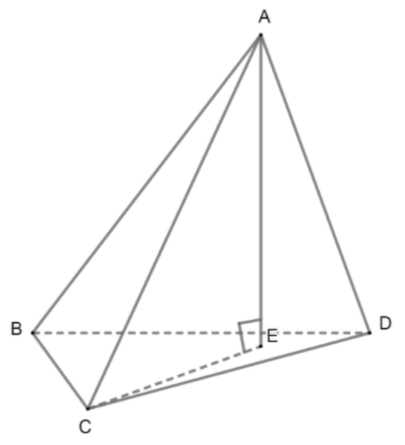
Now, ABCD is a triangular pyramid having base as the equilateral triangle BCD. ABC, ACD, and ABD are lateral faces. AE is the height of the pyramid. Now, let's consider the triangle BCD. Thus, we have,

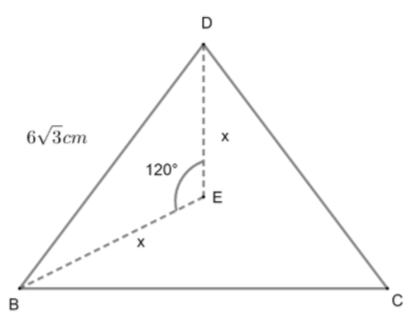
Now, we have to find the value of x. For this, we will find the \[\cos \,{{120}^{\circ }}\] using the sides given.
If a, b and c are the sides of the triangle and A is the angle included between b and c then:
\[\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}\]
Similarly, we have:
\[\begin{align}
  & \cos \,{{120}^{\circ }}=\dfrac{{{x}^{2}}+{{x}^{2}}-{{\left( 6\sqrt{3} \right)}^{2}}}{2\left( x \right)\left( x \right)} \\
 & \Rightarrow \dfrac{-1}{2}=\dfrac{2{{x}^{2}}-108}{2{{x}^{2}}} \\
 & \Rightarrow \dfrac{-1}{2}=\dfrac{{{x}^{2}}-54}{{{x}^{2}}} \\
\end{align}\]
\[\begin{align}
  & \Rightarrow -{{x}^{2}}=2{{x}^{2}}-108 \\
 & \Rightarrow 3{{x}^{2}}=108 \\
 & \Rightarrow {{x}^{2}}=\dfrac{108}{3} \\
 & \Rightarrow {{x}^{2}}=36 \\
 & \Rightarrow x=6\,cm \\
\end{align}\]

Therefore, \[\text{BE}=\text{CE}=\text{DE}=\text{6cm}\] Now, we consider the \[\Delta \text{ACE}\] As AE is the height, ACE is a right angled triangle as shown:

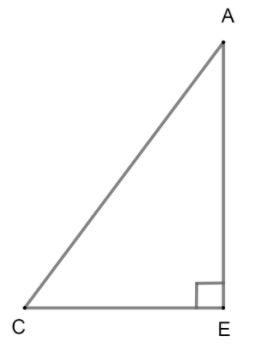
Now, we will apply the Pythagoras theorem in the right angled triangle ABC. According to this, if H is the hypotenuse, B is the base and P is the perpendicular then:
\[{{H}^{2}}={{P}^{2}}+{{B}^{2}}\]
In our case, \[\text{H}=\text{AC},\text{ P}=\text{AE and B}=\text{CE}\]. Thus:
\[\begin{align}
  & {{\left( AC \right)}^{2}}={{\left( AE \right)}^{2}}+{{\left( CE \right)}^{2}} \\
 & \Rightarrow {{\left( AC \right)}^{2}}={{\left( 4\,cm \right)}^{2}}+{{\left( 6\,cm \right)}^{2}} \\
 & \Rightarrow {{\left( AC \right)}^{2}}=16\,c{{m}^{2}}+36\,c{{m}^{2}} \\
 & \Rightarrow {{\left( AC \right)}^{2}}=52\,c{{m}^{2}} \\
 & \Rightarrow AC=2\sqrt{13}\,cm \\
\end{align}\]
Now, due to symmetry, \[AC=AB=AD=2\sqrt{13}\,cm\] now, we can say that all the lateral faces will have the same area because their dimensions are the same.
Area of a triangle with given sides: a, b and c is calculated by Heron's formula:
\[Area\,=\,\sqrt{S\left( S-a \right)\left( S-b \right)\left( S-c \right)}\]
Where, \[S=\dfrac{a+b+c}{2}\] in our case, \[a=2\sqrt{13},b=2\sqrt{13}\text{ and }c=6\sqrt{3}\]
In our case, \[S=\dfrac{2\sqrt{13}+2\sqrt{13}+6\sqrt{3}}{2}\Rightarrow \left( 2\sqrt{13}+3\sqrt{3} \right)cm\]
Thus, area of ABC:
\[\begin{align}
  & \text{Area of ABC=}\sqrt{\left( 2\sqrt{13}+3\sqrt{3} \right)\left[ \left( 2\sqrt{13}+3\sqrt{3} \right)-\left( 2\sqrt{13} \right) \right]\left[ \left( 2\sqrt{13}+3\sqrt{3} \right)-\left( 2\sqrt{13} \right) \right]\left[ 2\sqrt{13}+3\sqrt{3}-\left( 6\sqrt{3} \right) \right]} \\
 & \Rightarrow \text{Area of ABC=}\sqrt{\left( 2\sqrt{13}+3\sqrt{3} \right)\left( 3\sqrt{3} \right)\left( 3\sqrt{3} \right)\left( 2\sqrt{13}-3\sqrt{3} \right)} \\
 & \Rightarrow \text{Area of ABC=}\sqrt{\left( 2\sqrt{13}+3\sqrt{3} \right)\left( 2\sqrt{13}-3\sqrt{3} \right)\left( 3\sqrt{3} \right)\left( 3\sqrt{3} \right)} \\
 & \Rightarrow \text{Area of ABC=}\sqrt{\left[ {{\left( 2\sqrt{13} \right)}^{2}}-{{\left( 3\sqrt{3} \right)}^{2}} \right]{{\left( 3\sqrt{3} \right)}^{2}}} \\
 & \Rightarrow \text{Area of ABC=}\left( 3\sqrt{3} \right)\left( \sqrt{52-27} \right) \\
 & \Rightarrow \text{Area of ABC=}3\sqrt{3}\sqrt{25} \\
 & \Rightarrow \text{Area of ABC=}15\sqrt{3}\,c{{m}^{2}} \\
\end{align}\]
Thus, lateral surface area of the pyramid will be 3 times the area of ABC. Thus, we have:
Lateral surface area \[\Rightarrow 3\times \text{Area of ABC}\]
Lateral surface area \[\Rightarrow 3\times 15\sqrt{3}\,c{{m}^{2}}\]
Lateral surface area \[\Rightarrow 45\sqrt{3}\,c{{m}^{2}}\]
Now, we find the area of the base BCD:

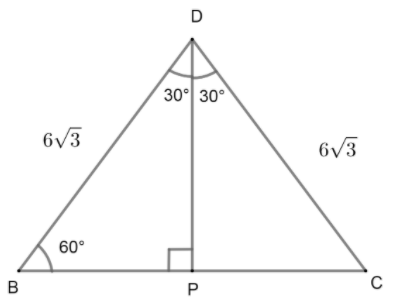
Here, DP is the height of the triangle BCD. Now, DP is the height of the triangle. From \[\Delta DBP\] we can say that:
\[\begin{align}
  & \sin \,{{60}^{\circ }}=\dfrac{DP}{DB} \\
 & \Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{DP}{6\sqrt{3}} \\
 & \Rightarrow \dfrac{6\sqrt{3}\times \sqrt{3}}{2}=DP \\
 & \Rightarrow DP=9\,cm \\
\end{align}\]
Now, the area of $\Delta BCD$ will be given by the product of base and height divided by 2. Thus,
\[\text{Area of }\Delta BCD=\dfrac{BC\times DP}{2}=\dfrac{6\sqrt{3}\times 9}{2}=27\sqrt{3}\,c{{m}^{2}}\]
Now, \[\text{Total area}=\text{Area of }\Delta BCD+\text{Lateral Surface Area}\]
\[\begin{align}
  & \Rightarrow \text{Total area}=27\sqrt{3}\,c{{m}^{2}}+45\sqrt{3}\,c{{m}^{2}} \\
 & \Rightarrow \text{Total area}=\left( 27+45 \right)\sqrt{3}\,c{{m}^{2}} \\
 & \Rightarrow \text{Total area}=72\sqrt{3}\,c{{m}^{2}} \\
\end{align}\]
Hence, option C is correct.

Note: While solving this question, we have assumed the ideal case. We have assumed that the apex is in the axis line of the pyramid. That's why, we have considered AE as the height, as it is an axis line and perpendicular to the base. This assumption is necessary, otherwise, we will not be able to calculate the area.