Question

The base of a triangle is axis of x and its other two sides are given by the equations \[y=\dfrac{1+\alpha }{\alpha }x+\left( 1+\alpha \right);y=\dfrac{1+\beta }{\beta }x+\left( 1+\beta \right)\]. Prove that the locus of its orthocentre is the line $x+y=0$.

Answer 1

Hint: Calwe first try to for the sides and the vertex of the triangle. Then using the perpendicular line theorem, we find the altitudes of the sides. We find the intersections of two sides which gives the locus of the orthocentre.

Complete step by step solution:
The base of a triangle is axis of x and its other two sides are given by the equations \[y=\dfrac{1+\alpha }{\alpha }x+\left( 1+\alpha \right);y=\dfrac{1+\beta }{\beta }x+\left( 1+\beta \right)\].
Let the triangle be $\Delta ABC$ whose base BC is the axis of x represented by $y=0$.
The intersection of the lines \[y=\dfrac{1+\alpha }{\alpha }x+\left( 1+\alpha \right);y=\dfrac{1+\beta }{\beta }x+\left( 1+\beta \right)\] is the vertex A.
We find the coordinates of the vertex. So, \[y=\dfrac{1+\alpha }{\alpha }x+\left( 1+\alpha \right)=\dfrac{1+\beta }{\beta }x+\left( 1+\beta \right)\]
This gives
\[\begin{align}
  & \dfrac{1+\alpha }{\alpha }x+\alpha =\dfrac{1+\beta }{\beta }x+\beta \\
 & \Rightarrow x\left( \dfrac{1}{\alpha }-\dfrac{1}{\beta } \right)=\beta -\alpha \\
 & \Rightarrow x\left( \dfrac{\beta -\alpha }{\alpha \beta } \right)=\beta -\alpha \\
 & \Rightarrow x=\alpha \beta \\
\end{align}\]
Putting the value of x we find the value of y.
So, \[y=\left( 1+\alpha \right)\beta +\left( 1+\alpha \right)=\left( 1+\beta \right)\left( 1+\alpha \right)\].
Therefore, the point is $A\equiv \left( \alpha \beta ,\left( 1+\beta \right)\left( 1+\alpha \right) \right)$.
Now we find the points B and C which are intersections of the given lines \[y=\dfrac{1+\alpha }{\alpha }x+\left( 1+\alpha \right);y=\dfrac{1+\beta }{\beta }x+\left( 1+\beta \right)\] with the line $y=0$.
Let the intersection with \[y=\dfrac{1+\alpha }{\alpha }x+\left( 1+\alpha \right)\] be point B which gives
\[\begin{align}
  & 0=\dfrac{1+\alpha }{\alpha }x+\left( 1+\alpha \right) \\
 & \Rightarrow x=-\alpha \\
\end{align}\]
The point B becomes $B\equiv \left( -\alpha ,0 \right)$.
Similarly point C becomes $C\equiv \left( -\beta ,0 \right)$.
Now we find the altitudes from the points A, B, C which has foot points on BC, AC, AB as D, E, F respectively.

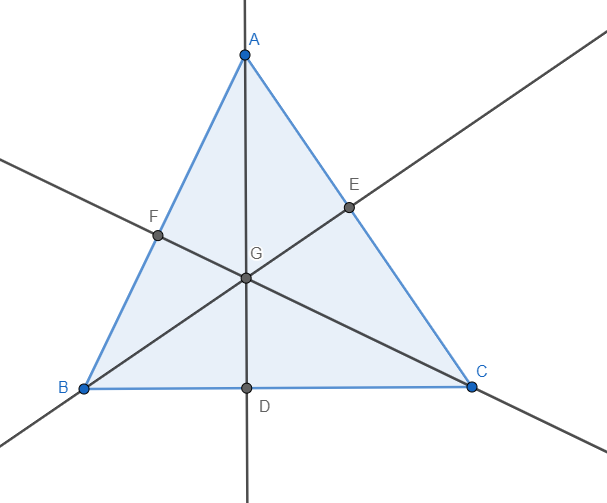
The equation of perpendicular line of $ax+by=k$ is $bx-ay=K$.
For line \[y=\dfrac{1+\alpha }{\alpha }x+\left( 1+\alpha \right)\], the perpendicular line is \[\dfrac{1+\alpha }{\alpha }y+x=K\] which goes through $C\equiv \left( -\beta ,0 \right)$.
So, putting the point we get \[\dfrac{1+\alpha }{\alpha }\times 0+\left( -\beta \right)=K\Rightarrow K=-\beta \].
The perpendicular line CF is
\[\begin{align}
  & \dfrac{1+\alpha }{\alpha }y+x=-\beta \\
 & \Rightarrow \left( 1+\alpha \right)y+\alpha x+\alpha \beta =0 \\
\end{align}\]
For line \[y=\dfrac{1+\beta }{\beta }x+\left( 1+\beta \right)\], the perpendicular line is \[\dfrac{1+\beta }{\beta }y+x=M\] which goes through $B\equiv \left( -\alpha ,0 \right)$.
So, putting the point we get \[\dfrac{1+\beta }{\beta }\times 0+\left( -\alpha \right)=M\Rightarrow M=-\alpha \].
The perpendicular line CF is
\[\begin{align}
  & \dfrac{1+\beta }{\beta }y+x=-\alpha \\
 & \Rightarrow \left( 1+\beta \right)y+\beta x+\alpha \beta =0 \\
\end{align}\]
These two lines intersect at orthocentre G whole locus will be the subtraction of the equations \[\left( 1+\alpha \right)y+\alpha x+\alpha \beta =0\] and \[\left( 1+\beta \right)y+\beta x+\alpha \beta =0\].
We get
\[\begin{align}
  & \left( 1+\alpha \right)y+\alpha x-\left( 1+\beta \right)y-\beta x=0 \\
 & \Rightarrow \left( \alpha -\beta \right)y+\left( \alpha -\beta \right)x=0 \\
 & \Rightarrow y+x=0 \\
\end{align}\]
Thus, proved that the locus of its orthocentre is the line $x+y=0$.

Note: We need to remember that the locus going through the orthocentre is the intersection of any two perpendicular lines drawn through the vertex. The perpendicular line of $y=0$ would have been $x=N$. We also could have used that lien to solve the problem.