Question

The battery of a car has an internal resistance of $0.1\Omega $ and an electromotive force of $12V$. When the battery is connected to the starter motor, the potential difference across the battery terminals will be $7V$. What will be the current supplied to the starter motor?
$\begin{align}
  & A.50A \\
 & B.70A \\
 & C.120A \\
 & D.190A \\
\end{align}$

Answer 1

Hint: First of all the current in the circuit is to be calculated. When the current is calculated, the internal resistance is to be taken care of. As the potential difference across the battery terminal has been given, we can equate the potential difference equation, which is the product of the current through the circuit and the resistance of the motor. These all may help you to solve this question.

Complete step-by-step solution:

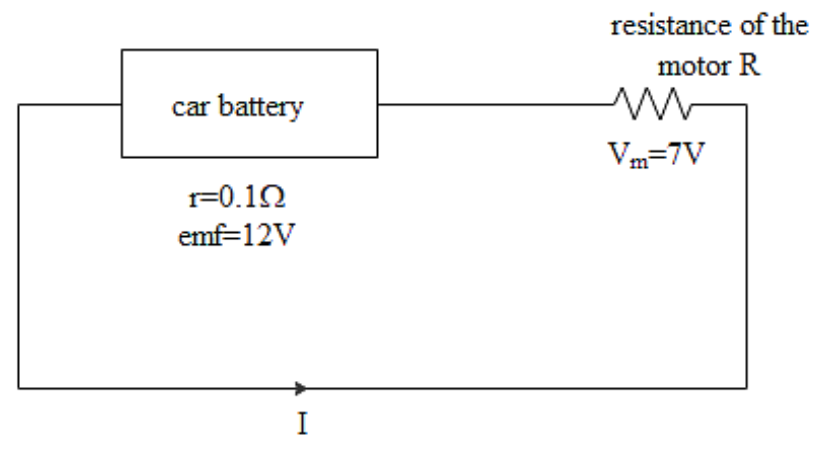
Let us suppose that the resistance of the motor is $R$. Therefore the current in the circuit will be given as,
$I=\dfrac{V}{R+r}$
Where $V$be the voltage in the circuit, $r$ be the internal resistance of the battery.
It is already mentioned in the question that,
$\begin{align}
  & V=12V \\
 & r=0.1\Omega \\
\end{align}$
So let us substitute this in the equation,
$I=\dfrac{12}{R+0.1}$
As the potential difference across the motor is given as
\[{{V}_{m}}=7V\]
We can write that,
\[\left( \dfrac{12}{0.1+R} \right)\times R=7V\]
Which is by the ohm’s law which gives the relation as,
\[V=IR\]
We can rearrange this equation and rewrite as,
\[12R=7\left( 0.1+R \right)\]
From this, the value of the resistance can be found,
That is,
\[\begin{align}
  & R=\dfrac{0.7}{5}\Omega \\
 & R=0.14\Omega \\
\end{align}\]
We obtained the value of resistance. Therefore now let us substitute this in the equation of current,
$\begin{align}
  & I=\dfrac{V}{R+r} \\
 & \because R=0.14\Omega \\
 & I=\dfrac{12}{0.1+0.14}A \\
 & I=50A \\
\end{align}$
Therefore, the correct answer has been obtained. The answer is given as option A.

Note: Ohm’s law states that the voltage in a circuit is proportional to the current flowing through the circuit. The proportionality used in this relation is known as resistance. The value of resistance depends on the length of the material, the area of the cross-section, and the nature of the material.