Question

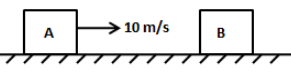
The blocks shown in the figure have equal masses. The surface of A is smooth but that of B has a friction coefficient of 0.10 with the floor. Block A is moving at a speed of 10 m/s towards B which is kept at rest. Find the distance travelled by B is (a) the collision is perfectly elastic and (b) the collision is perfectly inelastic. Take \[g = 10\,{\text{m/}}{{\text{s}}^2}\]

Answer 1

Hint: In both elastic and inelastic collision, the momentum of the system conserves. In a perfectly elastic collision, the colliding body comes to rest as soon as it collides with the second body. In inelastic collision, the two bodies after collision stick to each other. Use the law of conservation of momentum to determine the velocity of the second block. Use the law of conservation of energy for which the kinetic energy of the block is converted into thermal energy.

Formula used:
Momentum, \[p = mv\],
where, m is the mass and v is the velocity.
Kinetic energy, \[K = \dfrac{1}{2}m{v^2}\]
Thermal energy, \[E = \mu mgd\],
where, \[\mu \] is the coefficient of friction, g is the acceleration due to gravity and d is the distance.

Complete step by step answer:
We know that in both elastic and inelastic collisions, the momentum of the system conserves. Also, in inelastic collisions, the two bodies after collision stick to each other. Let initial velocity of the block A is \[{u_A}\], initial velocity of block B is \[{u_B}\], the final velocity after the collision of block A is \[{v_A}\] and that of B is \[{v_B}\].

(a) Using the law of conservation of momentum, we can write,
\[m{u_A} + m{u_B} = m{v_A} + m{v_B}\]
\[ \Rightarrow {u_A} + {u_B} = {v_A} + {v_B}\]
Since the block B is initially at rest, we can write,
\[{u_A} = {v_A} + {v_B}\]
Substituting \[{u_A} = 10\,{\text{m/s}}\] in the above equation, we get,
\[{v_A} + {v_B} = 10\] …… (1)
Also, for the elastic collision, we have,
\[{v_A} - {v_B} = - \left( {{u_A} - {u_B}} \right)\]
Substituting \[{u_A} = 10\,{\text{m/s}}\]and \[{u_B} = 0\] in the above equation, we get,
\[{v_A} - {v_B} = - \left( {10 - 0} \right)\]
\[ \Rightarrow {v_A} - {v_B} = - 10\] …… (2)
Subtracting equation (2) from (1), we get,
\[{v_A} + {v_B} - \left( {{v_A} - {v_B}} \right) = 10 - \left( { - 10} \right)\]
\[ \Rightarrow 2{v_B} = 20\]
\[ \Rightarrow {v_B} = 10\,{\text{m/s}}\]

Since the collision is perfectly elastic, the first block A will come at rest after the collision. Using the law of conservation of energy, the kinetic energy of the second block is converted into the thermal energy of block B.
\[\dfrac{1}{2}mv_B^2 = \mu mgd\]
\[ \Rightarrow \dfrac{1}{2}v_B^2 = \mu gd\]
Here, \[\mu \] is the coefficient of friction, g is the acceleration due to gravity and d is the distance moved by the block B.
Substituting \[{v_B} = 10\,{\text{m/s}}\], \[\mu = 0.10\] and \[g = 10\,{\text{m/}}{{\text{s}}^2}\] in the above equation, we get,
\[\dfrac{1}{2}{\left( {10} \right)^2} = \left( {0.10} \right)\left( {10} \right)d\]
\[ \therefore d = 50\,{\text{m}}\]

Thus, the block B will move a distance 50 m for the perfectly inelastic collision.

(b) For the perfectly inelastic collision, using the law of conservation of momentum, we can write,
\[m{u_A} + m{u_B} = \left( {m + m} \right)v\]
\[ \Rightarrow m{u_A} + m{u_B} = 2mv\]
\[ \Rightarrow {u_A} + {u_B} = 2v\]
Here, v is the velocity of the two blocks after the collision.
Substituting \[{u_A} = 10\,{\text{m/s}}\]and \[{u_B} = 0\] in the above equation, we get,
\[10 + 0 = 2v\]
\[ \Rightarrow v = 5\,{\text{m/s}}\]
Using the law of conservation of energy, we can write,
\[\dfrac{1}{2}\left( {2m} \right){v^2} = \mu \left( {2m} \right)gd\]
\[ \Rightarrow {v^2} = 2\mu gd\]
Substituting \[v = 5\,{\text{m/s}}\], \[\mu = 0.10\] and \[g = 10\,{\text{m/}}{{\text{s}}^2}\] in the above equation, we get,
\[{\left( 5 \right)^2} = 2\left( {0.10} \right)\left( {10} \right)d\]
\[ \therefore d = 12.5\,{\text{m}}\]

Thus, the block B will travel a distance of 12.5 m after the perfectly inelastic collision.

Note:The expression \[{v_A} - {v_B} = - \left( {{u_A} - {u_B}} \right)\] is derived by solving the expressions for law of conservation of momentum and law of conservation of energy. The derivation involves lots of calculation and therefore, students can simply remember this expression for perfectly elastic collision. The gravitational potential energy of both the blocks is zero since their distance from the ground is zero. The kinetic energy is converted into the thermal energy whenever the friction occurs in the motion. The coefficient of friction in the formula for the thermal energy is the kinetic friction coefficient and not static.