Question

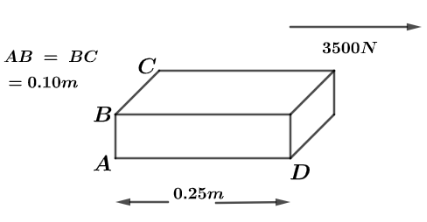
The brick shown in the diagram is glued to the floor. A $3500\,N$ force is applied to the top surface of the brick as shown in the figure. If the brick has shear modulus of $5.4 \times {10^9}\,N{m^{ - 2}}$ , how far to the right does the top face move relative to the stationary bottom face?

A. $5.8 \times {10^{ - 6}}\,m$
B. $2.6 \times {10^{ - 6}}\,m$
C. $1.1 \times {10^{ - 6}}\,m$
D. $6.5 \times {10^{ - 7}}\,m$

Answer 1

Hint: In order to solve this question, we will use the formula of shear modulus which is defined as the ratio of pressure and relative change in length of a material.Shear Modulus of elasticity is one of the measures of mechanical properties of solids. Other elastic moduli are Young’s modulus and bulk modulus.

Formula used:
Shear modulus denoted by,
$S = \dfrac{F}{A} \times \dfrac{x}{{\Delta x}}$
where, $\Delta x$ is the change in length from its initial length $x$.

Complete step by step answer:
Let us first find the area of the cross section which is given by multiplication of sides AD and AB .
$A = 0.25 \times 0.10\,{m^2}$
Given that, force is applied of magnitude $F = 3500\,N$
And original length of sectional area is given as AD, $x = 0.25\,m$
Now, we will use the formula of shear modulus to find the value of $\Delta x$ .
Magnitude of shear modulus is given by $S = 5.4 \times {10^9}N{m^{ - 2}}$
Putting these values in formula $S = \dfrac{F}{A} \times \dfrac{x}{{\Delta x}}$
$\Delta x = \dfrac{{Fx}}{{AS}}$
$\Rightarrow \Delta x = \dfrac{{3500 \times 0.25}}{{5.4 \times {{10}^9} \times 0.25 \times 0.10}}m$
$\therefore \Delta x = 6.5 \times {10^{ - 7}}m$
So, change in length became $\Delta x = 6.5 \times {10^{ - 7}}\,m$

Hence, the correct option is D.

Note:Theoretically, shear modulus can be understood as simply of how much shear stress needed to make a change in shear strain which is the ratio of stress and strain. It deforms the material into a new shape which is due to shear stress applied to its cross sectional areas. Its SI unit is simple as of Pressure given by $N{m^{ - 2}}$ .