
The center of gravity of a hollow cone of height h is at distance x from its vertex where the of x is:
Answer
507.6k+ views
Hint: Use the basic formula
Formula used:
Complete step-by-step solution:
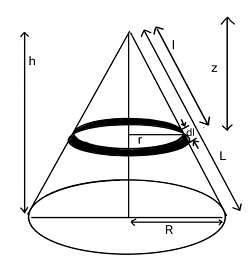
Let ‘x’ be the distance from the vertex of the cone to any point on the axis of the cone. Also let ‘R’ be the radius of the base of the cone. And ‘h’ is already given to be the height of the cone.
Let us take that, ‘r’ as the distance of any point on the cone from the axis of the cone, the distance being measured perpendicular to this axis.
From the picture, using the concept of geometry we can find that,
Here “l” is the distance of any point on the cone directly from the vertex. Looking at the image here gives you better understanding.
Let
The center of mass of a system is given by the formula,
Substituting the above values in the formula for center of mass, and using relations in equation (i), we obtain,
Cancelling the like terms, we get
On integrating numerator and denominator separately, we get
On applying the limits and simplifying, we get
After solving this, we obtain that,
So, this is the final answer.
Additional information:
If a person can hold an object by its center of gravity, then it will not rotate by the effect of gravity. Center of gravity is defined as the point about which the torques of gravity are zero. By definition it is not exactly the same with the center of mass. But in a field where the gravitational acceleration is uniform, the center of gravity coincides with the center of mass.
Note: Usually, the definition of center of mass contains summation where the masses are discreet. But in case of continuous mass distribution we have to use integration. In the integration, convert all the variables in a single variable and then put the limits.
Formula used:
Complete step-by-step solution:

Let ‘x’ be the distance from the vertex of the cone to any point on the axis of the cone. Also let ‘R’ be the radius of the base of the cone. And ‘h’ is already given to be the height of the cone.
Let us take that, ‘r’ as the distance of any point on the cone from the axis of the cone, the distance being measured perpendicular to this axis.
From the picture, using the concept of geometry we can find that,
Here “l” is the distance of any point on the cone directly from the vertex. Looking at the image here gives you better understanding.
Let
The center of mass of a system is given by the formula,
Substituting the above values in the formula for center of mass, and using relations in equation (i), we obtain,
Cancelling the like terms, we get
On integrating numerator and denominator separately, we get
On applying the limits and simplifying, we get
After solving this, we obtain that,
So, this is the final answer.
Additional information:
If a person can hold an object by its center of gravity, then it will not rotate by the effect of gravity. Center of gravity is defined as the point about which the torques of gravity are zero. By definition it is not exactly the same with the center of mass. But in a field where the gravitational acceleration is uniform, the center of gravity coincides with the center of mass.
Note: Usually, the definition of center of mass contains summation where the masses are discreet. But in case of continuous mass distribution we have to use integration. In the integration, convert all the variables in a single variable and then put the limits.
Latest Vedantu courses for you
Grade 11 Science PCM | CBSE | SCHOOL | English
CBSE (2025-26)
School Full course for CBSE students
₹41,848 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




