
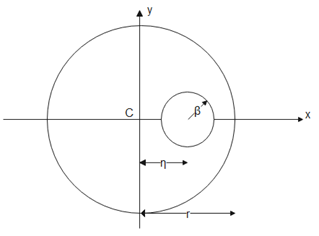
The centre of mass of a disc of uniform mass and radius r, when a circular portion of radius β has been removed from it such that centre of the hole is at distance η from the centre of disc is :

Answer
459.6k+ views
Hint: Center of mass is a point where total mass of an object is assumed to be concentrated. For uniformly distributed bodies usually the center of mass will be at its geometrical center. The main property of center of mass which we use here to solve this problem is that the moment of mass about the center of mass will be zero.
Formula used:
$\dfrac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}} = {x_{com}}$
Complete answer:
For the entire disc given the mass is distributed uniformly. So when we didn’t remove the portion the center of mass of the disc lies at the geometrical center of the disc, which is the origin in this case. It is clearly shown in below diagram
Let the mass of the remaining portion be ${m_1}$ and the mass of the removed portion be ${m_2}$. Let the area of the remaining portion be ${A_1}$ and the mass of the removed portion be ${A_2}$. Mass per unit area for the whole disc is constant everywhere. So mass will be proportional to area.
The center of mass of total disc is given as
$\dfrac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}} = {x_{com}}$
Here it originates. So ${x_{com}}$ is zero.
The area of remaining portion is ${A_1} = \pi {r^2} - \pi {\beta ^2}$ and the area of removed portion is ${A_2} = \pi {\beta ^2}$
Let ${x_1}$ be the position of the center of mass of the remaining part and ${x_2}$ be the center of mass of the removed part.
$\eqalign{
& {m_1}{x_1} + {m_2}{x_2} = 0 \cr
& \Rightarrow {A_1}{x_1} + {A_2}{x_2} = 0 \cr
& \Rightarrow {x_1} = - \dfrac{{{A_2}{x_2}}}{{{A_1}}} \cr
& \Rightarrow {x_1} = - \dfrac{{\left( {\pi {\beta ^2}} \right)\eta }}{{\pi {r^2} - \pi {\beta ^2}}} \cr
& \therefore {x_1} = - \dfrac{{\left( {{\beta ^2}} \right)\eta }}{{{r^2} - {\beta ^2}}} \cr} $
Hence $ - \dfrac{{\left( {{\beta ^2}} \right)\eta }}{{{r^2} - {\beta ^2}}}$ will be the position of center of mass of remaining portion.
Note:
The other way to do the same problem is assuming the total mass of the disc and something. We will find out the mass of the removed part and the mass of the remaining part in terms of mass of the whole disc. Then we will substitute in the center of mass formula to get the center of mass of the remaining part. But that will be a very long method.
Formula used:
$\dfrac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}} = {x_{com}}$
Complete answer:
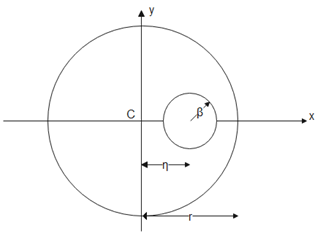
For the entire disc given the mass is distributed uniformly. So when we didn’t remove the portion the center of mass of the disc lies at the geometrical center of the disc, which is the origin in this case. It is clearly shown in below diagram

Let the mass of the remaining portion be ${m_1}$ and the mass of the removed portion be ${m_2}$. Let the area of the remaining portion be ${A_1}$ and the mass of the removed portion be ${A_2}$. Mass per unit area for the whole disc is constant everywhere. So mass will be proportional to area.
The center of mass of total disc is given as
$\dfrac{{{m_1}{x_1} + {m_2}{x_2}}}{{{m_1} + {m_2}}} = {x_{com}}$
Here it originates. So ${x_{com}}$ is zero.
The area of remaining portion is ${A_1} = \pi {r^2} - \pi {\beta ^2}$ and the area of removed portion is ${A_2} = \pi {\beta ^2}$
Let ${x_1}$ be the position of the center of mass of the remaining part and ${x_2}$ be the center of mass of the removed part.
$\eqalign{
& {m_1}{x_1} + {m_2}{x_2} = 0 \cr
& \Rightarrow {A_1}{x_1} + {A_2}{x_2} = 0 \cr
& \Rightarrow {x_1} = - \dfrac{{{A_2}{x_2}}}{{{A_1}}} \cr
& \Rightarrow {x_1} = - \dfrac{{\left( {\pi {\beta ^2}} \right)\eta }}{{\pi {r^2} - \pi {\beta ^2}}} \cr
& \therefore {x_1} = - \dfrac{{\left( {{\beta ^2}} \right)\eta }}{{{r^2} - {\beta ^2}}} \cr} $
Hence $ - \dfrac{{\left( {{\beta ^2}} \right)\eta }}{{{r^2} - {\beta ^2}}}$ will be the position of center of mass of remaining portion.
Note:
The other way to do the same problem is assuming the total mass of the disc and something. We will find out the mass of the removed part and the mass of the remaining part in terms of mass of the whole disc. Then we will substitute in the center of mass formula to get the center of mass of the remaining part. But that will be a very long method.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Explain sex determination in humans with the help of class 12 biology CBSE

What is pseudocoelom Where is it located class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

India is a sovereign socialist secular democratic republic class 12 social science CBSE

Draw a labeled diagram of an anatropous ovule and label class 12 biology CBSE




