
The centroid and a vertex of an equilateral triangle are
A)
B)
C)
D) None of these
Answer
531.9k+ views
Hint: Centroid is the intersection point of medians. Orthocentre is the intersection point of altitudes. Circumcentre is the intersection point of perpendicular bisectors of sides of a triangle.
In the case of an equilateral triangle, median, altitude, and perpendicular bisector are the same. Hence, centroid, circumcentre, and orthocentre coincide.
In the case of an equilateral triangle, we know that centroid, orthocentre, and circumcentre coincide.
We also know that the circumcentre is equidistant from the vertices.
So , in the case of an equilateral triangle, the centroid is equidistant from the vertices.
Now, the given centroid is
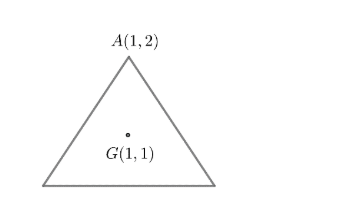
We, know the distance between two points
So,
So,
Now, since
Now, we know that the equation of a circle with center at
So, the equation of circumcircle becomes
So, the other two vertices should lie on this circle .
Now , we will check the options .
Option (a) :
We will substitute
On substituting
So ,
Option (b):
Now , we will substitute
On substituting
Which is false i.e.
So ,
Option (c):
Now , we will substitute
On substituting
Which is true i.e.
Hence ,
Therefore,
Option (a)
Note: The distance between two points
In the case of an equilateral triangle, median, altitude, and perpendicular bisector are the same. Hence, centroid, circumcentre, and orthocentre coincide.
In the case of an equilateral triangle, we know that centroid, orthocentre, and circumcentre coincide.
We also know that the circumcentre is equidistant from the vertices.
So , in the case of an equilateral triangle, the centroid is equidistant from the vertices.
Now, the given centroid is

We, know the distance between two points
So,
So,
Now, since
Now, we know that the equation of a circle with center at
So, the equation of circumcircle becomes
So, the other two vertices should lie on this circle .
Now , we will check the options .
Option (a) :
We will substitute
On substituting
So ,
Option (b):
Now , we will substitute
On substituting
Which is false i.e.
So ,
Option (c):
Now , we will substitute
On substituting
Which is true i.e.
Hence ,
Therefore,
Option (a)
Note: The distance between two points
Latest Vedantu courses for you
Grade 7 | CBSE | SCHOOL | English
Vedantu 7 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹45,300 per year
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




