Question

The change in the value of g at a height h above as the surface of the earth is the same at a depth d below the surface of the earth. When both d and h are much smaller than the radius of earth, then which one of the following is correct?
$\left( a \right)d=h$
$\left( b \right)d=2h$
$\left( c \right)d=\dfrac{3h}{2}$
$\left( d \right)d=\dfrac{h}{2}$

Answer 1

Hint: We will take the help of the formulas used for finding the value of gravity above and below earth’s surface along with the defined parameters. We will apply the condition discussed in the question about the same value of h and d where h is the height of the object to be calculated and d is the depth. Both h and d are very less than the radius of earth.

Formula used:
${{g}_{h}}=g\left( 1-\dfrac{2h}{R} \right),{{g}_{d}}=g\left( 1-\dfrac{d}{R} \right)$ where g is called gravity, h is the height of an object above earth’s surface, d is depth taken inside earth’s surface and R is radius of earth.

Complete step by step answer:
For this we are going to consider the following two diagrams which show earth’s variations with respect to gravity and height, explained in the figure.

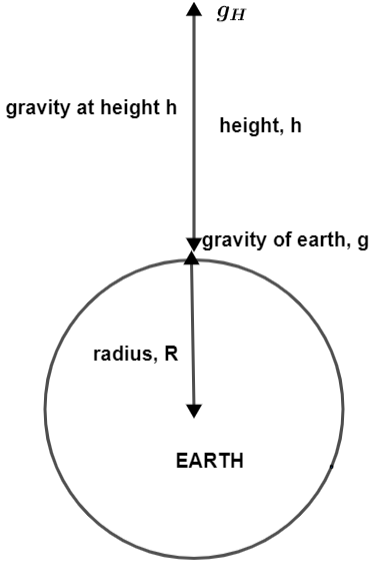
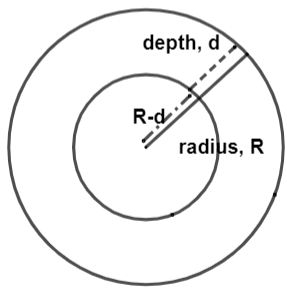
Suppose that the acceleration due to gravity at height h is represented as ${{g}_{h}}$ and due to depth d be ${{g}_{d}}$. We already know that the acceleration due to gravity on the earth’s surface is $g=\dfrac{GM}{{{r}^{2}}}$ where G is gravitational constant, R is radius of earth and M is mass of earth.
Aas the formula of gravitational force at height h is ${{g}_{h}}=g\left( 1-\dfrac{2h}{R} \right)$ or $g-{{g}_{h}}=\dfrac{2hg}{R}$ and the gravitational force at a height of h units is ${{g}_{d}}=g\left( 1-\dfrac{d}{R} \right)$ or $g-{{g}_{d}}=\dfrac{gd}{R}$ so, according to the question we will equate equation (i) and equation (ii) with each other and we will get

$\begin{align}
  & g-{{g}_{h}}=g-{{g}_{d}} \\
 & \Rightarrow \dfrac{2hg}{R}=\dfrac{gd}{R} \\
 & \Rightarrow 2h=d \\
\end{align}$

So, the correct answer is “Option B”.

Note:
The height above the earth’s surface has been selected to find gravity at that same height from the surface. This is useful in finding the value of gravity at that level exerted by any object that has been taken as an object. If we consider a depth inside the earth’s surface then, we will find the presence of gravity there also but the difference will be the slight change in the value which can be calculated by the given formula. Here, h << R because we are taking the height of an object above the surface of earth to be very less than the radius of the earth. Similarly, we have d << R. As by the statement in the question informing the value change of g at some height h taken above earth’s surface is the equal to the value change of gravity at some depth d downwards the earth’s surface.