
The chord joining two points ${\theta _1}{\text{ and }}{\theta _2}$on the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ such that $\tan {\theta _1}\tan {\theta _2} = - \dfrac{{{a^2}}}{{{b^2}}}$ will subtend a right angle at
$
(a){\text{ focus}} \\
(b){\text{ center}} \\
(c){\text{ end of the major axis}} \\
(d){\text{ end of the minor axis}} \\
$
Answer
119.1k+ views
Hint: In this question suppose two points ${\theta _1}$ and ${\theta _2}$ such that ${\theta _1} = \left( {a\cos {\theta _1},b\sin {\theta _1}} \right)$ and ${\theta _2} = \left( {a\cos {\theta _2},b\sin {\theta _2}} \right)$through which the chord passes. Then use the concept of slope of line passing through two given points to find the slope of $O{\theta _1}{\text{ and O}}{\theta _2}$ where O is the origin. Use the concept that if two lines are perpendicular then their slopes are related as ${m_1} \times {m_2} = - 1$.
Complete step-by-step answer:
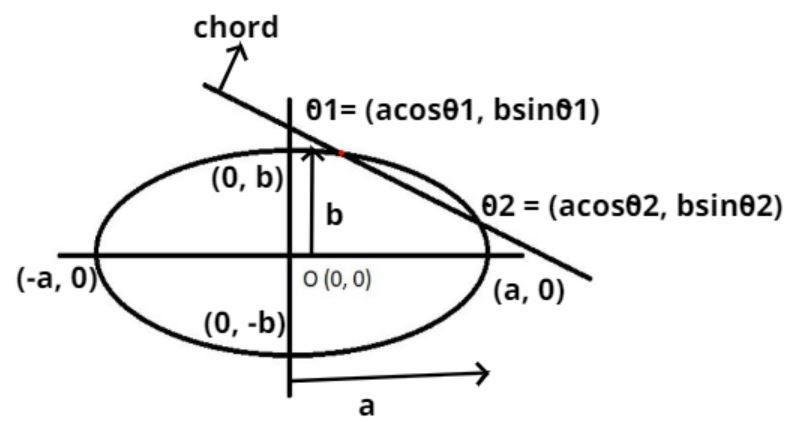
The chord joining two points $\left( {{\theta _1},{\theta _2}} \right)$ on the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ is shown above.
As we know that the ellipse is having a center (O) = (0, 0) is also shown in the figure.
Let us suppose the point ${\theta _1} = \left( {a\cos {\theta _1},b\sin {\theta _1}} \right)$ and ${\theta _2} = \left( {a\cos {\theta _2},b\sin {\theta _2}} \right)$ is also shown in the figure.
Now as we know that the slope between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given as
Slope (m) = $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
So find out the slopes of $\left( {O{\theta _1}} \right)$ and $\left( {O{\theta _2}} \right)$.
Let O = $(x_1, y_1)$ = (0, 0)
${\theta _1} = \left( {{x_2},{y_2}} \right) = \left( {a\cos {\theta _1},b\sin {\theta _1}} \right)$
${\theta _2} = \left( {{x_3},{y_3}} \right) = \left( {a\cos {\theta _2},b\sin {\theta _2}} \right)$
So let the slope of $\left( {0{\theta _1}} \right)$ be m1.
$ \Rightarrow {m_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{b\sin {\theta _1} - 0}}{{a\cos {\theta _1} - 0}} = \dfrac{b}{a}\tan {\theta _1}$
Now let the slope of $\left( {O{\theta _2}} \right)$ be m2.
$ \Rightarrow {m_1} = \dfrac{{{y_3} - {y_1}}}{{{x_3} - {x_1}}} = \dfrac{{b\sin {\theta _2} - 0}}{{a\cos {\theta _2} - 0}} = \dfrac{b}{a}\tan {\theta _2}$
Now multiply the slopes we have
$ \Rightarrow {m_1} \times {m_2} = \dfrac{b}{a}\tan {\theta _1} \times \dfrac{b}{a}\tan {\theta _2} = \dfrac{{{b^2}}}{{{a^2}}}\tan {\theta _1}\tan {\theta _2}$........................ (1)
Now it is given that
$\tan {\theta _1}\tan {\theta _2} = - \dfrac{{{a^2}}}{{{b^2}}}$
Now substitute this value in equation (1) we have,
$ \Rightarrow {m_1} \times {m_2} = \dfrac{{{b^2}}}{{{a^2}}}\tan {\theta _1}\tan {\theta _2} = \dfrac{{{b^2}}}{{{a^2}}} \times \dfrac{{ - {a^2}}}{{{b^2}}} = - 1$
So multiplication of slopes is (-1) which is the condition of the right angle.
Therefore the chord joining two points $\left( {{\theta _1},{\theta _2}} \right)$ on the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ will subtend a right angle at origin or center.
Hence option (B) is correct.
Note: The center of the given ellipse that is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ is (0, 0) that is the origin that’s why option (c) is correct. The equation of shifted ellipse or the ellipse whose center is not at origin is given by $\dfrac{{{{\left( {x - p} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - q} \right)}^2}}}{{{b^2}}} = 1$ here the center is at (p, q).
Complete step-by-step answer:

The chord joining two points $\left( {{\theta _1},{\theta _2}} \right)$ on the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ is shown above.
As we know that the ellipse is having a center (O) = (0, 0) is also shown in the figure.
Let us suppose the point ${\theta _1} = \left( {a\cos {\theta _1},b\sin {\theta _1}} \right)$ and ${\theta _2} = \left( {a\cos {\theta _2},b\sin {\theta _2}} \right)$ is also shown in the figure.
Now as we know that the slope between two points $(x_1, y_1)$ and $(x_2, y_2)$ is given as
Slope (m) = $\dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$
So find out the slopes of $\left( {O{\theta _1}} \right)$ and $\left( {O{\theta _2}} \right)$.
Let O = $(x_1, y_1)$ = (0, 0)
${\theta _1} = \left( {{x_2},{y_2}} \right) = \left( {a\cos {\theta _1},b\sin {\theta _1}} \right)$
${\theta _2} = \left( {{x_3},{y_3}} \right) = \left( {a\cos {\theta _2},b\sin {\theta _2}} \right)$
So let the slope of $\left( {0{\theta _1}} \right)$ be m1.
$ \Rightarrow {m_1} = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}} = \dfrac{{b\sin {\theta _1} - 0}}{{a\cos {\theta _1} - 0}} = \dfrac{b}{a}\tan {\theta _1}$
Now let the slope of $\left( {O{\theta _2}} \right)$ be m2.
$ \Rightarrow {m_1} = \dfrac{{{y_3} - {y_1}}}{{{x_3} - {x_1}}} = \dfrac{{b\sin {\theta _2} - 0}}{{a\cos {\theta _2} - 0}} = \dfrac{b}{a}\tan {\theta _2}$
Now multiply the slopes we have
$ \Rightarrow {m_1} \times {m_2} = \dfrac{b}{a}\tan {\theta _1} \times \dfrac{b}{a}\tan {\theta _2} = \dfrac{{{b^2}}}{{{a^2}}}\tan {\theta _1}\tan {\theta _2}$........................ (1)
Now it is given that
$\tan {\theta _1}\tan {\theta _2} = - \dfrac{{{a^2}}}{{{b^2}}}$
Now substitute this value in equation (1) we have,
$ \Rightarrow {m_1} \times {m_2} = \dfrac{{{b^2}}}{{{a^2}}}\tan {\theta _1}\tan {\theta _2} = \dfrac{{{b^2}}}{{{a^2}}} \times \dfrac{{ - {a^2}}}{{{b^2}}} = - 1$
So multiplication of slopes is (-1) which is the condition of the right angle.
Therefore the chord joining two points $\left( {{\theta _1},{\theta _2}} \right)$ on the ellipse $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ will subtend a right angle at origin or center.
Hence option (B) is correct.
Note: The center of the given ellipse that is $\dfrac{{{x^2}}}{{{a^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$ is (0, 0) that is the origin that’s why option (c) is correct. The equation of shifted ellipse or the ellipse whose center is not at origin is given by $\dfrac{{{{\left( {x - p} \right)}^2}}}{{{a^2}}} + \dfrac{{{{\left( {y - q} \right)}^2}}}{{{b^2}}} = 1$ here the center is at (p, q).
Recently Updated Pages
Difference Between Mutually Exclusive and Independent Events

Difference Between Area and Volume

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main 2025 Helpline Numbers - Center Contact, Phone Number, Address

Trending doubts
JEE Main 2025: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Chemistry Question Paper with Answer Keys and Solutions

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Other Pages
NCERT Solutions for Class 11 Maths Chapter 9 Straight Lines

NCERT Solutions for Class 11 Maths Chapter 8 Sequences and Series

NCERT Solutions for Class 11 Maths Chapter 10 Conic Sections

NCERT Solutions for Class 11 Maths Chapter 13 Statistics

NCERT Solutions for Class 11 Maths Chapter 12 Limits and Derivatives

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs




