
The clock shows 6:50 as the time in the morning. The angle between the minutes hand and the hours hand is X. It represents which kind of an angle?
Answer
547.5k+ views
Hint: The clock reads 6:50 a.m. We have to check what kind of angle the hour hand and the minute hand is making. It is acute angle or obtuse angle or right angle or straight angle. We usually take the help of a compass but now we should just compare and be able to come to a conclusion.
Complete step-by-step solution:
Acute angle is kind of angle which means less than ${{90}^{\circ }}$ where ${{0}^{\circ }}<\alpha <{{90}^{\circ }}$.
Right angle is the kind of angle which is equal to ${{90}^{\circ }}$ where $\alpha ={{90}^{\circ }}$.
Obtuse angle is the kind of which measures greater than ${{90}^{\circ }}$ and less than ${{180}^{\circ }}$ where ${{90}^{\circ }}<\alpha <{{180}^{\circ }}$.
Straight angle is the kind of angle which is equal to ${{180}^{\circ }}$ where $\alpha ={{180}^{\circ }}$.
The reading of 6:50 as the time in the morning can be represented as
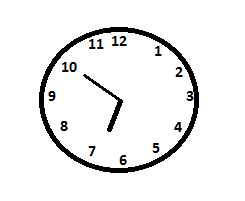
We know that the total angle around the connecting midpoint is ${{360}^{\circ }}$. This angle is for the whole 12 numbers in the clock.
The difference between the number 7 and 10 is $10-7=3$.
As the reading has yet not reached 7:00. The hour hand is behind the 7.
Using unitary system, we get for 12 numbers the angle is ${{360}^{\circ }}$ which means for 3 numbers it will be $\dfrac{{{360}^{\circ }}\times 3}{12}={{90}^{\circ }}$.
Now as the hour hand is still yet to reach mark 7 the angle will be greater than ${{90}^{\circ }}$ but obviously less than ${{180}^{\circ }}$ as it doesn’t cover total 6 marks.
So, if the angle is $\alpha $ then ${{90}^{\circ }}<\alpha <{{180}^{\circ }}$.
So, it is an obtuse angle.
Note: We should always know the definition of all angles. It would make our problem easier. We should be able to estimate roughly the angle between lines without needing a compass. This can be only done through practice.
Complete step-by-step solution:
Acute angle is kind of angle which means less than ${{90}^{\circ }}$ where ${{0}^{\circ }}<\alpha <{{90}^{\circ }}$.
Right angle is the kind of angle which is equal to ${{90}^{\circ }}$ where $\alpha ={{90}^{\circ }}$.
Obtuse angle is the kind of which measures greater than ${{90}^{\circ }}$ and less than ${{180}^{\circ }}$ where ${{90}^{\circ }}<\alpha <{{180}^{\circ }}$.
Straight angle is the kind of angle which is equal to ${{180}^{\circ }}$ where $\alpha ={{180}^{\circ }}$.
The reading of 6:50 as the time in the morning can be represented as

We know that the total angle around the connecting midpoint is ${{360}^{\circ }}$. This angle is for the whole 12 numbers in the clock.
The difference between the number 7 and 10 is $10-7=3$.
As the reading has yet not reached 7:00. The hour hand is behind the 7.
Using unitary system, we get for 12 numbers the angle is ${{360}^{\circ }}$ which means for 3 numbers it will be $\dfrac{{{360}^{\circ }}\times 3}{12}={{90}^{\circ }}$.
Now as the hour hand is still yet to reach mark 7 the angle will be greater than ${{90}^{\circ }}$ but obviously less than ${{180}^{\circ }}$ as it doesn’t cover total 6 marks.
So, if the angle is $\alpha $ then ${{90}^{\circ }}<\alpha <{{180}^{\circ }}$.
So, it is an obtuse angle.
Note: We should always know the definition of all angles. It would make our problem easier. We should be able to estimate roughly the angle between lines without needing a compass. This can be only done through practice.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

A moving boat is observed from the top of a 150 m high class 10 maths CBSE




