
The coefficient of linear expansion of a cubical crystal along three mutually perpendicular directions is
Answer
381.3k+ views
Hint: You may start with a cuboid and set the temperature to rise from
Complete answer:
Considering a cubical crystal structure
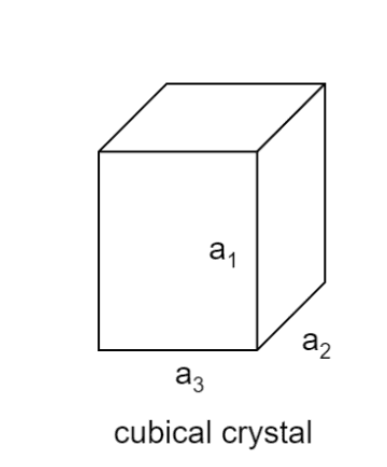
Let
We know for linear expansion
Where
Take the temperature of the solid above to rise from
So for all the edges we have
After expansion, their product will give the volume of the cuboid at temperature
However, we know that the cuboid's initial volume is determined by the product of the edges. That is to say,
By neglecting small values from the above equation we get
Now using the formula of volume expansion
Comparing this from the above equation we get
Note:
Thermal expansion is the phrase used to describe the tendency of matter to change in length, area, and volume as a result of temperature changes. When molecules are heated, they move and vibrate more, increasing the space between them. The ratio of relative expansion to temperature change can be characterised as the coefficient of thermal expansion.
Complete answer:
Considering a cubical crystal structure

Let
We know for linear expansion
Where
Take the temperature of the solid above to rise from
So for all the edges we have
After expansion, their product will give the volume of the cuboid at temperature
However, we know that the cuboid's initial volume is determined by the product of the edges. That is to say,
By neglecting small values from the above equation we get
Now using the formula of volume expansion
Comparing this from the above equation we get
Note:
Thermal expansion is the phrase used to describe the tendency of matter to change in length, area, and volume as a result of temperature changes. When molecules are heated, they move and vibrate more, increasing the space between them. The ratio of relative expansion to temperature change can be characterised as the coefficient of thermal expansion.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




