Question

The consecutive angles of a parallelogram are
A. equal
B. complementary
C. supplementary
D. none of these.

Answer 1

Hint:
We can suppose one figure of the parallelogram and using the properties of the parallelogram can find the sum of the two consecutive angles. If the sum is $ 90^\circ $ then they are complementary and if it is $ 180^\circ $ then it will be supplementary.

Complete step by step solution:
Here we are told to find the relation between the consecutive angles of the parallelogram. We must know what parallelogram is. It is the quadrilateral in which both the opposite sides are parallel and equal. We need to know what complementary and supplementary means, if the sum of the angles is $ 90^\circ $ then the angles are said to be complementary and if the sum of the angels is $ 180^\circ $ then they are supplementary.
So we need to find the sum of any two consecutive angles of the parallelogram.
Let us suppose $ ABCD $ is a parallelogram and $ E $ is the point if we extend the line $ AB $

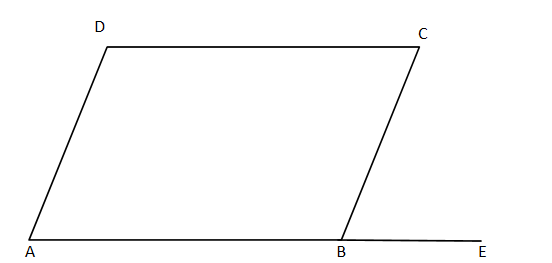
Now we need to find the sum of any two consecutive angles say $ \angle DAB{\text{ and }}\angle ABC $
Now we know that this is a parallelogram so we can say that $ AB\parallel CD{\text{ and BC}}\parallel DA $
Hence we can say that $ \angle DAB = \angle CBE $ (corresponding angles of the two parallel sides are equal)
So we get $ \angle DAB = \angle CBE $ $ - - - - (1) $
As $ \angle CBA{\text{ and }}\angle CBE $ lie on the straight line so we know that the sum must be equal to $ 180^\circ $
So we can say that
 $ \angle CBA + \angle CBE = 180^\circ - - - - - - (2) $
Now substituting the value of $ \angle CBE $ from equation (1) in equation (2) we get
 $ \angle CBA + \angle DAB = 180^\circ $
Hence we get the sum of the two consecutive angles to be $ 180^\circ $
So they are supplementary.

Hence option C is correct.

Note:
Here we must know what supplementary and complementary angles mean. Properties of all types of quadrilaterals must be the one student must be clear with to solve such types of problems easily.