Question

The constant quantity in uniform circular motion is:
a) Linear Speed
b) Centripetal Force
c) Acceleration
d) Momentum

Answer 1

Hint: The direction of occurrence of a particular quantity is of utmost importance in a circular motion. Many quantities in a uniform circular motion become variable only because the direction of a particular parameter changes. We will check for the change in direction of the respective parameters to find out our answer.

Complete step by step answer:
In a uniform circular motion, an object keeps on revolving around a fixed axis or fixed point at constant speed. Circular motion becomes a little difficult as we include vectors in them. As we know the speed of the object remains constant but not the velocity! Velocity is nothing but the speed of the body along with the direction of motion. Although the speed remains constant throughout the circular motion, the direction of motion keeps on changing every instant. Thus the velocity keeps on changing every instant.

A simple depiction of a body in uniform circular motion is as follows:

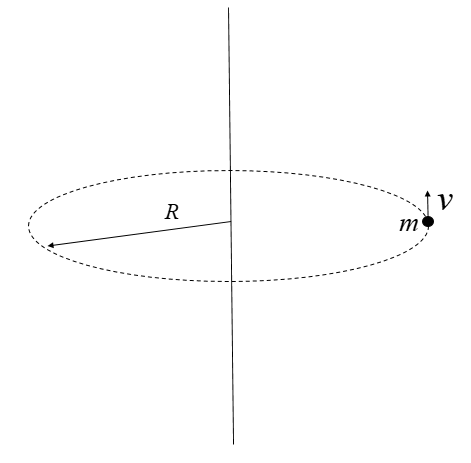
In a uniform circular motion, although the velocity of the body changes but the angular velocity of the body remains fixed.
We know that the centrifugal force is given by:
$F=\dfrac{m{{v}^{2}}}{r}$
Where, $m$ is the mass of the body, $r$ is the radius of the circular path and $v$ is the velocity of the body. Since we squared the velocity, the change in its direction stops playing any role, and hence, ${{v}^{2}}$also becomes constant.
Hence, the centrifugal force on the body also remains the same.
We also know that the linear momentum of a body is given by:
$p=mv$
Where, clearly, there is no change in the mass of the body but the velocity of the body keeps on changing every instant. Thus, the linear momentum of the body also changes every moment.
We know that acceleration is nothing but the change in velocity of the body. Also, the velocity of the body keeps on changing every moment. Hence the acceleration also keeps on changing every moment.
Now, the angular momentum of the body is given by:
$L=r\times p$
$\Rightarrow L=|r||p|\sin \theta $
Here, we know that the radius makes a constant angle of $90{}^\circ $ with linear momentum. This means that $\sin \theta $ is constant. Also, $|p|$ and $|r|$ are also constants. Hence, the angular momentum of the body remains constant.

So, the correct answer is “Option D”.

Note: In a uniform circular motion, there are more than one parameter which remains constant. It is the change in direction of vector quantities which makes any given quantity variable rather than constant. Some constant quantities in a uniform circular motion are speed of body, the kinetic energy of the body, angular momentum of the body and mass of the body.