
The correct graph between the frequency
(A)
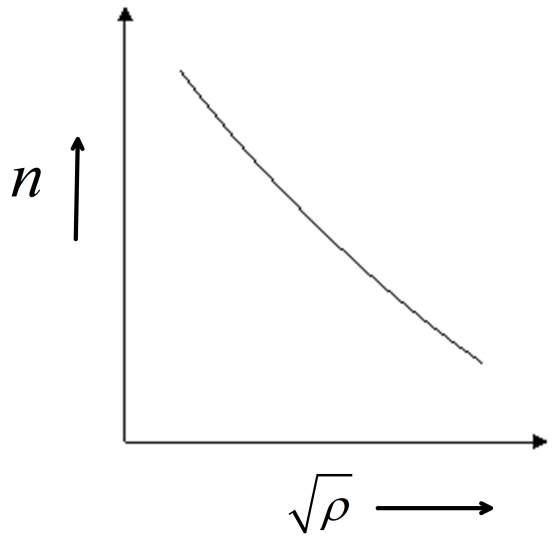
(B)
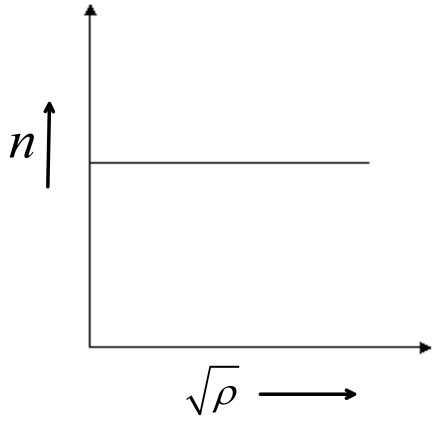
(C)
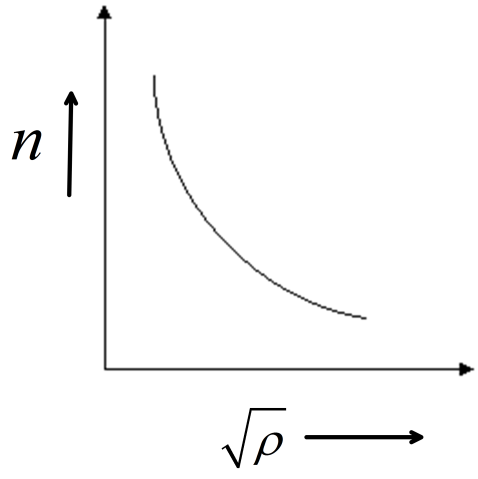
(D)
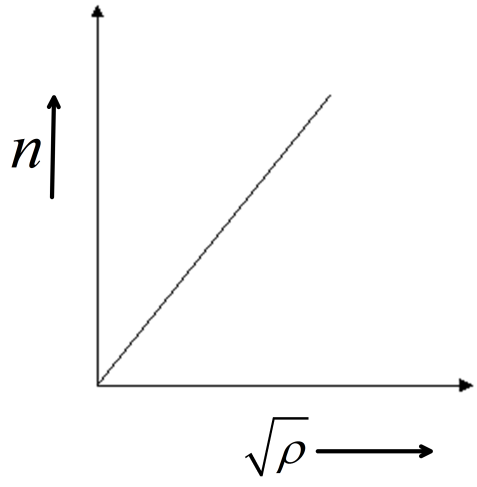




Answer
439.2k+ views
1 likes
Hint :Observe the formula for frequency of transverse vibration in a stretched string. It is known that the frequency of
Complete Step By Step Answer:
We know that the, frequency of
So, if we keep the tension of the string, length of the string and radius of the stretched string then for say
where
So, we can write,
So, frequency is inversely proportional to the square root of density of the material.
This signifies an equation of hyperbola. Hence, the plot between frequency of the string and the square root of density
Option (C ) signifies a graph of a hyperbola.
Hence, option (c ) is correct.
Note :
This relation between frequency of the stretched string and the square root of the density of the wire is known as the Law of density for transverse vibration in stretched string. It states that, if length, radius and tension of the wire is kept constant then frequency of transverse vibration will be inversely proportional to the square root of density of the wire.
Complete Step By Step Answer:
We know that the, frequency of
So, if we keep the tension of the string, length of the string and radius of the stretched string then for say
where
So, we can write,
So, frequency is inversely proportional to the square root of density of the material.
This signifies an equation of hyperbola. Hence, the plot between frequency of the string and the square root of density
Option (C ) signifies a graph of a hyperbola.
Hence, option (c ) is correct.
Note :
This relation between frequency of the stretched string and the square root of the density of the wire is known as the Law of density for transverse vibration in stretched string. It states that, if length, radius and tension of the wire is kept constant then frequency of transverse vibration will be inversely proportional to the square root of density of the wire.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




