Question

The crescent shaded in the diagram, is like that found on many flags. PSR is an arc of a circle O and radius 24.0 cm. Angle $POR={{48.2}^{\circ }}$. PQR is a semicircle on PR as diameter, where $PR=19.6cm\left[ \pi =3.14 \right]\left[ \cos 24.1=0.91 \right]$
The area of the crescent is
A.116.4 $cm^2$
B.123.4 $cm^2$
C.112.2 $cm^2$
D.23.4 $cm^2$
 

Answer 1

Hint: Here we have to find the area of the crescent. For that, we will first draw the figure with the required points given. Then we will find the area of the sector POR. We will then calculate the area of the triangle POR and area of the semicircle. We will get the area of the crescent by subtracting the area of area of the triangle POR and area of the semicircle from the area of the sector.

Complete step-by-step answer:
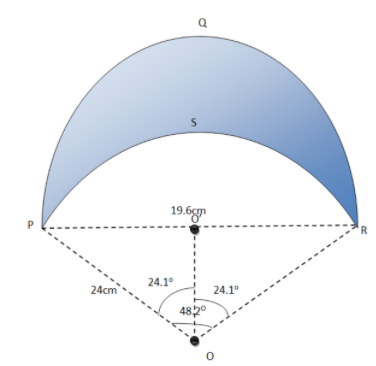
Let’s first draw the labeled figure of crescent.
We will first find the area of sector PORS and radius OR is given which is 24 cm and $\angle POR={{48.2}^{\circ }}$
 We know the area of sector$=\dfrac{\theta }{360}\times \pi {{r}^{2}}$
Here r is the radius and is the angle subtended by the arc.
Therefore, area of sector PORS $=\dfrac{48.2}{360}\times \pi {{\left( 24 \right)}^{2}}$
We will put the value of $\pi $here.
$\Rightarrow$ $\dfrac{48.2}{360}\times 3.14\times {{\left( 24 \right)}^{2}}$
On further simplification, we get
Area of sector PORS $=242.16c{{m}^{2}}$
In $\vartriangle O'OR$
Height of the triangle is OO’ and OR is equal to 24 cm.
Therefore,
$OO'=\cos {{24.1}^{\circ }}\times 24$
As it is given that ${\cos 24.1 = 0.91}$
On putting the value and evaluating, we get
$OO'=21.91cm$
We will calculate the area of $\vartriangle POR$
We know, area of triangle $\dfrac{1}{2}\times b\times h$
In $\vartriangle POR$
$\begin{align}
  & b=19.6cm \\
 & h=21.91cm \\
\end{align}$
Therefore, Area of $\vartriangle POR=\dfrac{1}{2}\times 19.6\times 21.91$
On further Simplification, we get
$\Rightarrow$ $\text{area of }\vartriangle POR=214.70c{{m}^{2}}$
We will calculate the area of semicircle PQR.
Area of semicircle PQR$=\dfrac{\pi {{\left( 9.8 \right)}^{2}}}{2}$
On further evaluation, we get
Area of semicircle PQR$=150.859c{{m}^{2}}$
Now,
$\Rightarrow$ $\text{area of crescent}=\text{area of semicircle}-\left( \text{area of sector }PORS-\text{area of}\vartriangle POR \right)$
Putting value of area of triangle POR, area of sector PORS and area of semicircle, we get
$\Rightarrow$ $\text{area of crescent}=150.859-\left( 242.16-214.70 \right)$
Subtracting the numbers, we get
$\Rightarrow$ $\text{area of crescent}=123.4c{{m}^{2}}$
Thus, the correct answer is option B.

Note: We have calculated the area of the crescent. We need to know about it to solve such problems. A crescent is a curved shape which is thicker in the middle and thinner near the two ends, it looks like the little sliver of moon we might notice in the sky.