Question

The critical angle of glass-air interface is (given ${{\mu }_{glass}}=1.5$)
A.$24{}^\circ $
B.$48{}^\circ $
C.$42{}^\circ $
D.$45{}^\circ $

Answer 1

Hint: Firstly, you could recall the definition of critical angle. Now recall the expression for Snell’s law and then substitute accordingly as per the definition of critical angle and thus derive the required expression. Then in the expression for critical angle substitute the refractive indices and thus get the answer.

Formula used:
Snell’s law,
${{n}_{i}}\sin i={{n}_{r}}\sin r$

Complete answer:
In the question we are asked to find the critical angle of glass-air interface. We are also given the value of refractive index of glass in the question as,
${{\mu }_{glass}}=1.5$ ……………………………………………………. (1)
As a first step, let us recall what exactly the critical angle of an interface is. Critical angle is that angle at which a light ray is incident on the interface so as to result in an angle of refraction of $90{}^\circ $. The value of this critical angle varies with different combinations of materials on each side of the boundary or an interface. We could derive the expression for critical angle from Snell's law. We know that Snell’s law is given by,
${{n}_{i}}\sin i={{n}_{r}}\sin r$
Where, ${{n}_{i}}$ and ${{n}_{r}}$ are the refractive indices of incident and refractive medium, $i$ and $r$ are the incident and refracted angle.

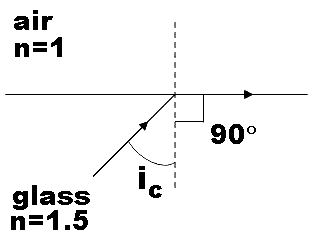
For critical angle, Snell’s law becomes,
${{n}_{i}}\sin {{i}_{c}}={{n}_{r}}\sin 90$
$\Rightarrow \sin {{i}_{c}}=\dfrac{{{n}_{r}}}{{{n}_{i}}}\left( 1 \right)$
$\therefore {{i}_{c}}={{\sin }^{-1}}\left( \dfrac{{{n}_{r}}}{{{n}_{i}}} \right)$ …………………………………………….. (2)
Now that we have derived the expression for critical angle, let us substitute accordingly to get the answer. Also, the ray should be traveling from denser medium to rarer medium to satisfy this relation.
So,
${{n}_{i}}={{n}_{glass}}=1.5$
${{n}_{r}}={{n}_{air}}=1$
From (2),
${{i}_{c}}={{\sin }^{-1}}\left( \dfrac{1}{1.5} \right)$
$\Rightarrow {{i}_{c}}={{\sin }^{-1}}\left( 0.67 \right)$
$\therefore {{i}_{c}}=42{}^\circ $
Therefore, we found the critical angle of the glass-air interface to be $42{}^\circ $.

Hence,option C would be the correct answer.

Note:
In case, if you are wondering why critical angle is applicable only for rays traveling from denser medium, we could justify this by using the expression for critical angle. Consider the ray traveling from rarer to denser medium, this would mean that ${{n}_{r}}\rangle {{n}_{i}}$, so the ratio $\dfrac{{{n}_{r}}}{{{n}_{i}}}$ will obviously be greater than 1. As sine of a number can never be greater than 1, this case is impossible.