
The cross-section of a canal is in the form of a trapezium. If the canal top is 10 m wide and the bottom is 6 m wide, and the area of cross-section is 72 sq. m, then the depth of the canal is
A) 10 m
B) 7 m
C) 6 m
D) 9 m
Answer
488.7k+ views
Hint:
It is given that; the cross-section of a canal is in the form of a trapezium and the canal top is 10 m wide and the bottom is 6 m wide and the area of the well is 72 sq. m.
Let d be the depth of the well.
Thus, by using the formula for area of trapezium,
Hence, the depth of the canal can be found.
Complete step by step solution:
It is given that; the cross-section of a canal is in the form of a trapezium and the canal top is 10 m wide and the bottom is 6 m wide.
Let a be the length of canal top, b be the length of the bottom part and h be the depth of the canal.
Thus, we get
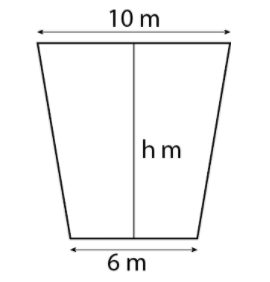
Also, the area of the cross-section is 72 sq. m. So,
Now, area of trapezium is given by
Substituting
Thus, we get the depth of the canal as 9 m.
Note:
Alternate Method:
It is given that; the cross-section of a canal is in the form of a trapezium and the canal top is 10 m wide and the bottom is 6 m wide.
Let the depth of the canal be h m.
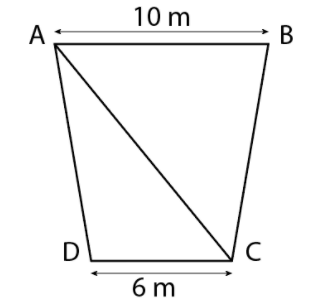
So, we can find the area of the trapezium from the above diagram as the sum of area of triangle ABC and area of triangle ADC.
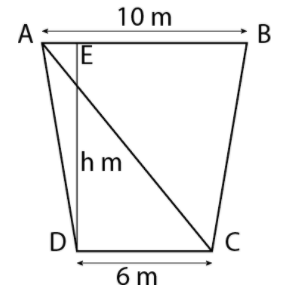
From above diagram,
Also, the area of the cross-section is 72 sq. m. So,
Thus, we get the depth of the canal as 9 m.
It is given that; the cross-section of a canal is in the form of a trapezium and the canal top is 10 m wide and the bottom is 6 m wide and the area of the well is 72 sq. m.
Let d be the depth of the well.
Thus, by using the formula for area of trapezium,
Hence, the depth of the canal can be found.
Complete step by step solution:
It is given that; the cross-section of a canal is in the form of a trapezium and the canal top is 10 m wide and the bottom is 6 m wide.
Let a be the length of canal top, b be the length of the bottom part and h be the depth of the canal.
Thus, we get

Also, the area of the cross-section is 72 sq. m. So,
Now, area of trapezium is given by
Substituting
Thus, we get the depth of the canal as 9 m.
Note:
Alternate Method:
It is given that; the cross-section of a canal is in the form of a trapezium and the canal top is 10 m wide and the bottom is 6 m wide.
Let the depth of the canal be h m.

So, we can find the area of the trapezium from the above diagram as the sum of area of triangle ABC and area of triangle ADC.

From above diagram,
Also, the area of the cross-section is 72 sq. m. So,
Thus, we get the depth of the canal as 9 m.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Where did Netaji set up the INA headquarters A Yangon class 10 social studies CBSE

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The British separated Burma Myanmar from India in 1935 class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What are the public facilities provided by the government? Also explain each facility




