Question

The diagonals of a rectangle are perpendicular to each other.
(a). True
(b). False
(c). Only when the rectangle is also a rhombus.
(d). None of these.

Answer 1

- Hint: Draw a rectangle, with diagonals. From the figure, find out if the diagonals are perpendicular to each other or not, if they are then the statement is true or else the statement is false.

Complete step-by-step answer: -
Consider the rectangle ABCD drawn below.

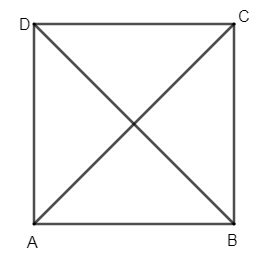
 We know that a rectangle has 2 diagonals. From the figure we can see that AC and BD are the diagonals of the rectangle ABCD. From the figure we can understand that each one is a line segment drawn between the opposite corners of the rectangle. The diagonals of the rectangle are equal i.e. AC = BD and they bisect each other. But the diagonals are not perpendicular to each other. We know that if diagonals are perpendicular then they cut at $${90}^{\circ }$$. But in the rectangle the diagonals don’t cut at $${90}^{\circ }$$. Thus the statement given is false.
If in case of square and rhombus, the diagonals are perpendicular to each other. But for rectangles, parallelograms, trapeziums the diagonals are not perpendicular.
$$\therefore$$ The diagonals of a rectangle are not perpendicular to each other. The given statement is false.
 $$\therefore$$ Option (b) is the correct answer.

Note: If you are having doubt about the diagonals if they are perpendicular or not always draw a figure and confirm it. If we draw a rectangle with diagonals, we can see that they are not perpendicular. If we draw a square, their diagonals are always perpendicular.