
The diagonals of a rhombus bisect each other at
(a)
(b)
(c)
(d)
Answer
531.6k+ views
Hint: Rhombus is a quadrilateral with four equal sides whose diagonals bisect each other. Take any two adjacent triangles formed by the intersection of the diagonals and try to prove them congruent. Use the property that the measure of a straight angle is
Complete step-by-step answer:
As we know the property of rhombus that all sides of the rhombus are equal to each other and diagonals bisect each other and here we need to determine the angle formed by the diagonals at the intersecting point.
So, let we have a rhombus ABCD which diagram can be given as :-
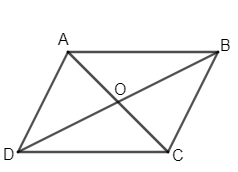
So, the sides AB, BC, CD and AD are equal to each other and diagonals AC and BD bisecting each other i.e. length AO is equal to CO and BO is equal to DO.
So, we have
So, from the given diagram, we have to prove angles
In
Hence,
Now, we know that the sum of angles formed by a line on a line is
It means the angles in the diagram below sum as
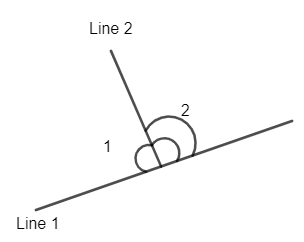
So,
Hence, from the rhombus, the sum of angles
Now, from the equation (iv), we have
So, we can re-write equation (v) as
Hence,
Now, we know pairs of vertically opposite angles are always equal formed by intersection of two lines.
It means, we get from the rhombus ABCD as
Hence,
So, the diagonals of rhombus bisect each other at
Hence, option (c) is correct.
Note: One may take any two triangles from the pairs
Use the fundamental properties of a rhombus and don’t get confused with the properties of rectangle, parallelogram or square. All have some common properties and some different properties as well. So, be clear with the properties of a rhombus to solve these kinds of problems.
Complete step-by-step answer:
As we know the property of rhombus that all sides of the rhombus are equal to each other and diagonals bisect each other and here we need to determine the angle formed by the diagonals at the intersecting point.
So, let we have a rhombus ABCD which diagram can be given as :-

So, the sides AB, BC, CD and AD are equal to each other and diagonals AC and BD bisecting each other i.e. length AO is equal to CO and BO is equal to DO.
So, we have
So, from the given diagram, we have to prove angles
In
Hence,
Now, we know that the sum of angles formed by a line on a line is
It means the angles in the diagram below sum as

So,
Hence, from the rhombus, the sum of angles
Now, from the equation (iv), we have
So, we can re-write equation (v) as
Hence,
Now, we know pairs of vertically opposite angles are always equal formed by intersection of two lines.
It means, we get from the rhombus ABCD as
Hence,
So, the diagonals of rhombus bisect each other at
Hence, option (c) is correct.
Note: One may take any two triangles from the pairs
Use the fundamental properties of a rhombus and don’t get confused with the properties of rectangle, parallelogram or square. All have some common properties and some different properties as well. So, be clear with the properties of a rhombus to solve these kinds of problems.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Discuss the main reasons for poverty in India




