Question

The diagonals of a rhombus bisect each other at ________angles.
A. Acute
B. Obtuse
C. Right
D. None

Answer 1

Hint: In this question is given that we have to find at what angles the diagonals of a rhombus bisects each other, so to find the solution first of all we need to draw a rhombus ABCD where AC and BD are the diagonals which interests each other at E.

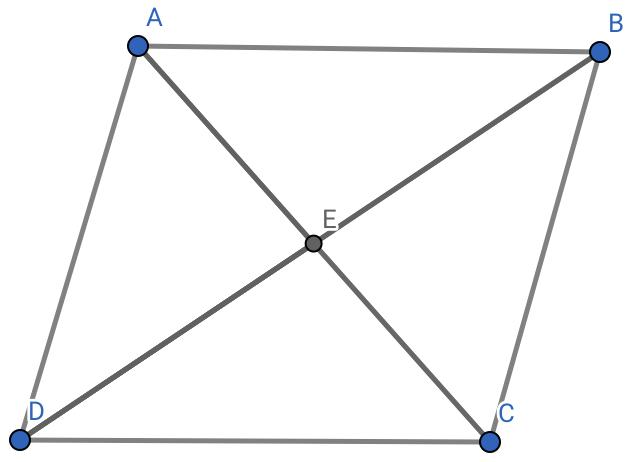
For a rhombus AE=EC and BE=ED.

Complete step-by-step answer:
We know that the diagonals of a parallelogram bisect each other.
Also we know that every rhombus is a parallelogram, but the main difference is every side of a rhombus is equal, i.e, AB=BC=CD=DA.
Now for $$\triangle CDE\ and\ \triangle CBE$$, we have,
CD=CB [Sides of a rhombus]
BE=ED [ since, diagonals bisects each other]
CE=CE [ common side]
So by SSS congruence (side-side-side) property, we can say that,
$$\triangle CDE\ congruent\ to\ \triangle CBE$$
i.e,$$\triangle CDE\ \cong \ \triangle CBE$$
As we know that ‘CPCT rule: if two or more triangles are congruent, then all of their corresponding angles and sides are congruent’
So by CPCT we can say that,
$$\angle CED\ =\ \angle CEB$$ ………..equation (1)

Since $$\angle CED\ and\ \angle CEB$$ are linear pairs so the summation of the angles is $$180^\circ$$.
i.e, $$\angle CED+\angle CEB=180^\circ$$
$$\Rightarrow \angle CEB+\angle CEB=180^\circ$$ [by using equation(1)]
$$\Rightarrow 2\ \angle CEB=180^\circ$$
$$\Rightarrow \angle CEB=\dfrac{180^\circ }{2}$$
$$\Rightarrow \angle CEB=90^\circ$$
Now by equation (1) we can write,
$$\angle CED=\angle CEB=90^\circ$$
Hence, the diagonals of a rhombus bisect each other at right angles.
So the correct option id option C.


Note: So to solve this type of problem you need to know that a rhombus is also a parallelogram but for a rhombus the corresponding sides are equal to each other, and also diagonals of a rhombus perpendicularly bisects each other.