Question

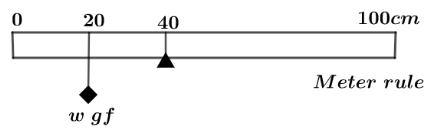
The diagram alongside shows a uniform meter rule of weight \[100\,gf\] being balanced on a knife edge placed at the $40\,cm$ mark, by suspending a weight $w$ at the mark $20\,cm$ ,find:
(a) The value of $w$.
(b) The resultant moment and its direction if the weight $w$ is moved to the mark $30\,cm$.
(c) The position of another weight of $50\,gf$ to balance the rule.

Answer 1

Hint: In order to solve this question, we will use the concept of principle of moments. Which states that in equilibrium state of forces the clockwise moment about a point is always equal to its anticlockwise moment. Moment is the product of force and perpendicular stable distance point of suspension.

Complete step by step answer:
(a) Let us first find the clockwise moment about weight $w$

Is given by, $100 \times {d_1}$ where $100$ is the mass of the ruler and ${d_1} = (50 - 40) = 10cm$ which is the distance from centre of mass to the balancing point knife edge.
Clockwise moment $ = 100 \times 10 \to (i)$
Now, an anticlockwise moment is given as, $w \times {d_2}$ where ${d_2}$ is the distance between weight and knife edge point.
Anticlockwise moment $ = w \times 20 \to (ii)$
Comparing both equations $(i)and(ii)$ we get,
$w = \dfrac{{1000}}{{20}}g$
$\therefore w = 50\,g$

Hence, the unknown weight is $w = 50\,g$.

(b) If weight is now moved to the point $30\,cm$ then, the meter ruler will try to bend in clockwise direction. So calculating the moment about the mark $30\,cm$ is given by $w \times d$ where $w = 50\,g$ and $d$ is the distance between knife edge and weight.
$d = 40 - 30 = 10cm$
Moment $ = 50 \times 10$
Moment $ = 500\,gcm$ in anticlockwise direction.

(c) Let the position of new weight $50\,gf$ is at a distance of $x$ cm from left and this weight must be placed after the knife edge so to produce an anticlockwise moment hence balancing the ruler.
Since, we have anticlockwise Moment $ = 500gcm \to (i)$ in Clockwise direction.
And, calculating clockwise moment as:
$1000 + 50(x - 40) \to (ii)$
Equating both equations $(i)and(ii)$ we get,
$1500 = 50x$
$\therefore x = 30\,cm$

Hence, the new weight $50\,gf$ must be placed at a point of $30\,cm$ from the left.

Note:Principle of moment is based upon the concept that a weight tends to produce an anticlockwise moment about its equilibrium point this makes system unstable and hence if it’s placed in such a point where its clockwise moment will just equals to the anticlockwise moment, system will remain in equilibrium as long as the positions of weights don’t changes.