Question

The diagram below shows a lever in use. Without changing the dimensions of the lever, if the load is shifted towards the fulcrum what happens to the mechanical advantage of the lever?

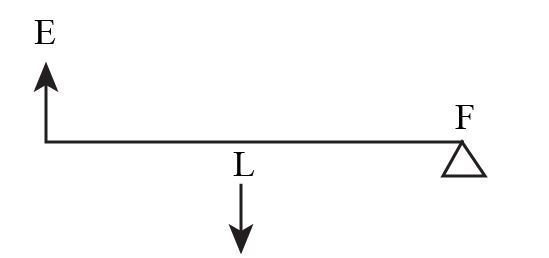
Answer 1

Hint: We all know that leverage is helpful in various mechanical engineering fields just to reduce the effort required from either side which can be implemented by increasing the distance from the fulcrum or pivot.

Complete Step-by-step Solution
We are all familiar with the concept that Mechanical advantage is the force multiplication technique. It is the relation which tells us what is the value of the input force that is applied by the machine and what value of the effort we get as an output from the machine.
Refer to the figure given below:

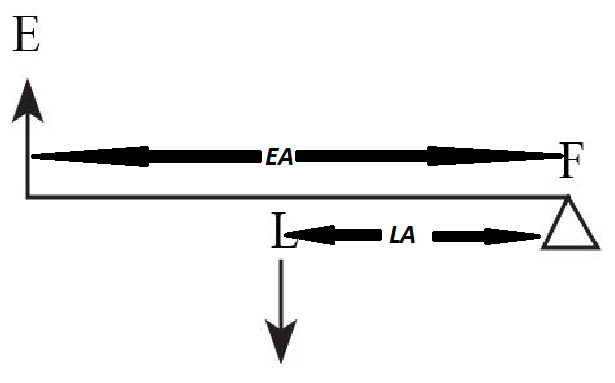
The diagram shows that the load $L$ is between the effort $E$ and fulcrum $F$. Taking the moment of forces through the fulcrum $F$. Hence it comes out to be,
$E \times EA = L \times L$
$\dfrac{{EA}}{{LA}} = \dfrac{L}{E}$
Here $LA$ is the load arm and $EA$ is the effort arm.
We know that Mechanical advantage is given by,
$MA = \dfrac{{EA}}{{LA}}$
Here $MA$ is the mechanical advantage.
Therefore, if the load $L$ is moved towards, the fulcrum so the load arm decreases, and hence the Mechanical Advantage increases.

Therefore, the mechanical advantage increases.

Note:
Mechanical advantage is the calculation of the amplification of the force that is achieved by a mechanical tool or device. Mechanical advantage should not be confused with efficiency as a mechanical advantage could be greater than one but efficiency can’t be greater than one. Efficiency is the ratio of output energy obtained to the input energy supplied but Mechanical advantage is the ratio of output effort i.e. force to the input effort.