Question

The diagram below shows four orange spheres moving in circular paths at constant speeds. The speeds are indicated by the red arrows. The radius of the circular path for each is indicated by the green arrows. The mass of each sphere is labeled inside the boundary of the sphere.
How do the spheres rank, according to the magnitudes of the net force acting on them, greatest first?

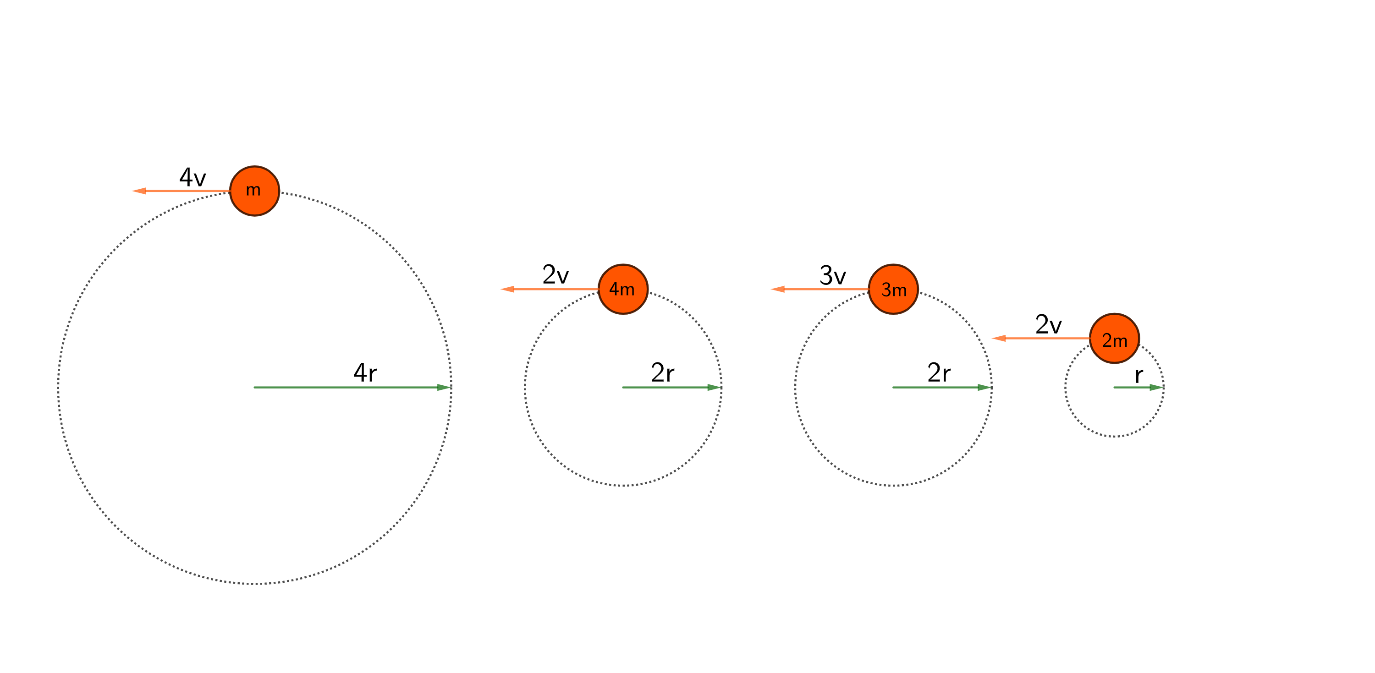
(A) $ \text{4,3,1 and 2 tie} $
(B) $ \text{3,1 and 4 tie,2} $
(C) $ \text{3,2 and 4 tie,1} $
(D) $ \text{1,2 and 3 tie,4} $
(E) $ \text{1,3,2,4} $

Answer 1

Hint :As the spheres are moving in a circular path, the net force acting on them is the centripetal force acting in the tangential direction. The centripetal force depends on the mass of the rotating body, velocity of the rotating body, and the radius of the circular path, in which the body is moving which is expressed as $ F=\dfrac{M{{V}^{2}}}{R} $

Complete Step By Step Answer:
When an object rotates in a circular orbit, a force tangential at every point acts on it which tends to remove the object from the circular path which is known as centripetal force.
The centripetal force depends upon the mass of the object, the velocity of the object, and the radius of the circular path followed by the object.
The centripetal force can be calculated by the formula,
 $ F=\dfrac{M{{V}^{2}}}{R} $
Where, $ M $ is the mass of the object,
 $ V $ is the velocity of the object
 $ R $ is the radius of the orbit of the object.
Now, let us calculate the centripetal force for every given case individually
Case (I)
The given values are $ M=m $ , $ V=4v $ , and $ R=4r $
Substituting these values in the equation of force,
 $ {{F}_{1}}=\dfrac{m{{(4v)}^{2}}}{4r} $
 $ \therefore {{F}_{1}}=4\dfrac{m{{v}^{2}}}{r} $
Case (II)
The given values are $ M=4m $ , $ V=2v $ , and $ R=2r $
Substituting these values in the equation of force,
 $ {{F}_{2}}=\dfrac{4m{{(2v)}^{2}}}{2r} $
 $ \therefore {{F}_{2}}=8\dfrac{m{{v}^{2}}}{r} $
Case (III)
The given values are $ M=3m $ , $ V=3v $ , and $ R=2r $
Substituting these values in the equation of force,
 $ {{F}_{3}}=\dfrac{3m{{(3v)}^{2}}}{2r} $
 $ \therefore {{F}_{3}}=13.5\dfrac{m{{v}^{2}}}{r} $
Case (IV)
The given values are $ M=2m $ , $ V=2v $ , and $ R=r $
Substituting these values in the equation of force,
 $ {{F}_{4}}=\dfrac{2m{{(2v)}^{2}}}{r} $
 $ \therefore {{F}_{4}}=8\dfrac{m{{v}^{2}}}{r} $
From the above cases, $ F_3 $ is the greatest and $ F_1 $ is the smallest and $ F_2 $ and $ F_4 $ are equal
Hence, the correct answer is Option $ (C) $ .

Note :
From here we can understand that force acting on a body revolving in a circle also known as centripetal force is proportional to the mass of the object, proportional to the square of the velocity, and inversely proportional to the radius of the orbit. Hence, to get more centripetal force, the mass and velocity of the object should be more and the radius of the orbit should be less.