Question

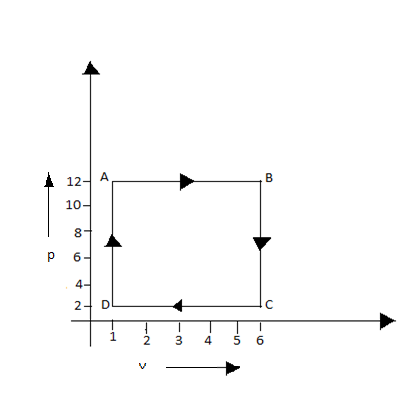
The diagram shown is a P-V graph of thermodynamic behavior of an ideal gas. Find out from this graph (I) work done in the process A $ \to $B, B$ \to $ C, C$ \to $D and D$ \to $A. (II) Work done in the complete cycle A$ \to $B$ \to $C$ \to $D$ \to $A.

Answer 1

Hint: Work done is defined by the product of pressure exerted and change in volume. Therefore the work done is given as: W = P$\Delta V$
Where, p is pressure and $\Delta V$ is change in volume ( ${V_{final}} - {V_{initial}}$).

Complete step by step answer:
The work done is given by W = P$\Delta V$. Here understanding sign convention is very important to solve problems like this.
- If the process is expansion the work done by gas will give negative sign convention.
          W = - P$\Delta V$
-If the process is contraction the work done on gas will give a positive sign convention.
            W = + P$\Delta V$

Let's solve the problem
(i) - Work done in process A $ \to $B, from the graph we can make out that pressure is constant in this process. Always when pressure is constant there will be change in volume. Therefore the process is expansion.
W = - P$\Delta V$
        = - ($12 \times {10^5}$)($5 \times {10^{ - 3}}$)
        = -6000J

- Work done in process B$ \to $ C, from the graph we can make out that volume remains constant so the work done in this process is 0.

- Work done in process C$ \to $D, from the graph we can make out that pressure is constant and there is a change in volume. Here the process carried out is contraction.
  W = + P$\Delta V$
        = + ($2 \times {10^5}$)($5 \times {10^{ - 3}}$)
        = 1000J

- Work done process D$ \to $A, from the graph we can make sure that the volume is kept constant. Thus the work done is zero.

(ii) the work done in complete cycle = sum of work done in process A $ \to $B, B$ \to $ C, C$ \to $D and D$ \to $A
                                                                  = 6000J + 0J + 1000J + 0J
                                                                  = 7000J
      Thus the work done in complete cycle is 7000J
So, the correct answer is “Option B”.

Note: If the process is expansion the work done is by gas so the sign convention is negative as, when work is done by the gas some energy is let out. If the process is contraction the work done is on gas so the sign convention is positive as, when work is done on the system there will be addition of energy to the system.