Question

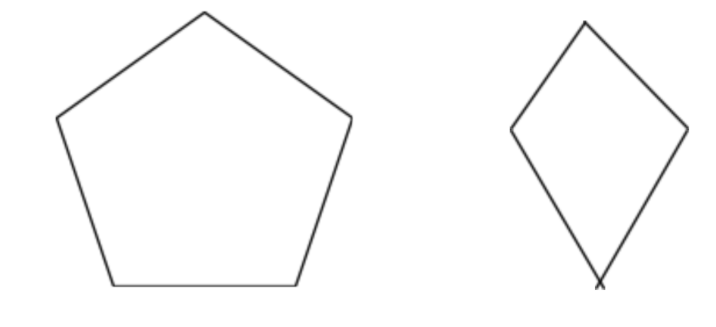
The diagram shows a regular pentagon and a kite.
Complete the following statement.
The kite has rotational symmetry of order

Answer 1

Hint: A kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. The kites are the quadrilaterals that have an axis of symmetry along one of their diagonals. Rotational symmetry, also known as radial symmetry, is the property a shape has when it looks the same after some rotation by a partial turn.

Complete step-by-step answer:
Kite: A kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. The kites are the quadrilaterals that have an axis of symmetry along one of their diagonals. Every kite is orthodiagonal, meaning that its two diagonals are at right angles to each other. Moreover, one of the two diagonals (the symmetry axis) is the perpendicular bisector of the other, and is also the angle bisector of the two angles it meets.
Rotational symmetry : Rotational symmetry, also known as radial symmetry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation. Formally the rotational symmetry is symmetry with respect to some or all rotations in m-dimensional Euclidean space.
The kite has rotational symmetry of order one.
So, the correct answer is “1”.

Note: Regular polygons have the same number of lines of symmetry as there are sides of the polygon. . An object's degree of rotational symmetry is the number of distinct orientations in which it looks exactly the same for each rotation.