Question

The diagram shows a square JKLM drawn on a grid of equal squares with side 1 unit. W, X, Y are three moving points in the diagram. On the diagram, draw
a) The locus of the point X which is at 4 units away from KL.
b) The locus of the point Y which is at 6 units away from M.
Hence mark with the symbol $\otimes $, the intersection of locus of X and locus of Y.

Answer 1

Hint: To solve this question, we should know the distance between a point and a line and distance between two points. We know that the distance between a point $\left( {{x}_{1}},{{y}_{1}} \right)$and a line $ax+by+c=0$ is given by the formula $\text{distance}=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$. We know that the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$. In our question, by assuming the point M as origin, we can write the coordinates of other corners. By using the above formulae and simplifying them, we get the required locus. After getting the locus, we should solve them to get the intersection point.

Complete step by step answer:
We are given a square grid which has 8 small squares on each side. SO, the length of each side of the larger square is 8 units. Let us assume that the corner M is origin and the lines ML and MJ are along x and y axis respectively.
So, we can write the coordinates of the corners as
$M\left( 0,0 \right),J\left( 0,8 \right),K\left( 8,8 \right),L\left( 8,0 \right)$.
We know that the line KL is parallel to the y-axis. Any line parallel to y-axis is of the form $x=k$. So, we can write the equation of the line KL as $x=8\Rightarrow x-8=0\to \left( 1 \right)$
Let us assume the coordinates of the point X as $\left( {{x}_{1}},{{y}_{1}} \right)$. We are given that it is at a constant distance of 4 units from the line KL.
We know that the distance between a point $\left( {{x}_{1}},{{y}_{1}} \right)$and a line $ax+by+c=0$ is given by the formula $\text{distance}=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$.
Using this with the point $X\left( {{x}_{1}},{{y}_{1}} \right)$ and the line KL $x-8=0$ and distance = 4 units, we get
$\begin{align}
  & \text{4}=\dfrac{\left| {{x}_{1}}-8 \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\
 & \left| {{x}_{1}}-8 \right|=4 \\
\end{align}$
Removing the modulus sign, we get a plus or minus sign.
\[\begin{align}
  & {{x}_{1}}-8=\pm 4 \\
 & {{x}_{1}}-8=4\Rightarrow {{x}_{1}}=12 \\
 & {{x}_{1}}-8=-4\Rightarrow {{x}_{1}}=4 \\
 & {{x}_{1}}=4\text{ or 12} \\
\end{align}\]
We know that ${{x}_{1}}=12$ is outside the area that is given to us. So, we get the locus of X as
${{x}_{1}}=4\Rightarrow x=4\to \left( 2 \right)$.
It is a straight line parallel to x-axis.
Let us assume the coordinates of the point Y as $\left( {{x}_{2}},{{y}_{2}} \right)$. We are given that it is at a constant distance of 6 units from the point M.
We know that the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right),\left( {{x}_{2}},{{y}_{2}} \right)$ is $\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$.
Using this on the points Y and M, we get
$6=\sqrt{{{\left( {{x}_{1}}-0 \right)}^{2}}+{{\left( {{y}_{1}}-0 \right)}^{2}}}$
By squaring on both sides, we get
\[\begin{align}
  & {{6}^{2}}={{\left( \sqrt{{{\left( {{x}_{1}}-0 \right)}^{2}}+{{\left( {{y}_{1}}-0 \right)}^{2}}} \right)}^{2}} \\
 & {{x}_{1}}^{2}+{{y}_{1}}^{2}={{6}^{2}} \\
\end{align}\]
So, the locus of Y is ${{x}^{2}}+{{y}^{2}}={{6}^{2}}\to \left( 3 \right)$. It is a circle with a centre at M and a radius of 6 units.
By drawing them on the diagram, we get

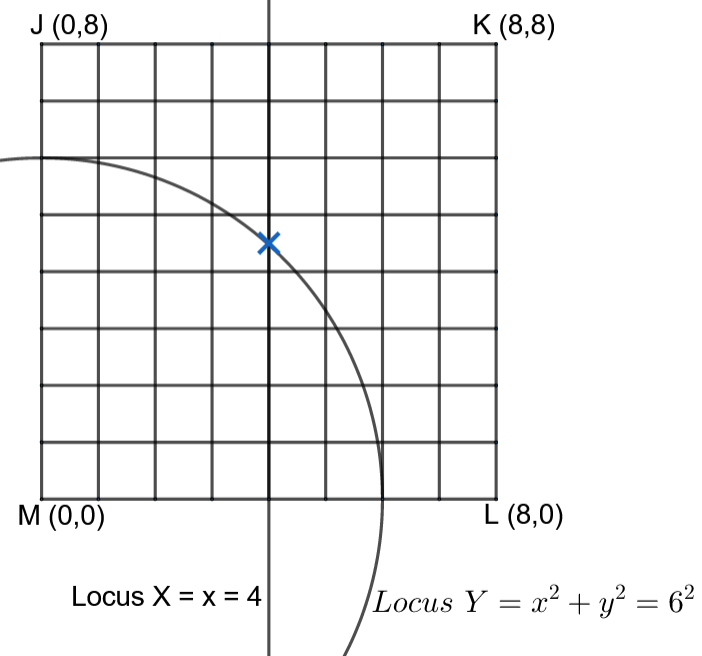
The point with the $\times $ mark is the point of intersection of the two locus. TO get the point of intersection, we should solve both the equations 2 and 3. Using the equation-2 $x=4 $ in equation-3, we get
$\begin{align}
  & {{4}^{2}}+{{y}^{2}}={{6}^{2}} \\
 & {{y}^{2}}=36-16=20 \\
 & y=\sqrt{20}=2\sqrt{5} \\
\end{align}$
Y is written as positive because only positive y is allowed in our diagram. So, the point of intersection is $P\left( 4,2\sqrt{5} \right)$.
$\therefore $Hence, we have derived the required locus and the point of intersection.

Note: We can remember a general result from this question. The first result is that the locus of a point which is at a certain distance from a line is another line parallel to the given line. The second result is that the locus of a point which is at a certain distance from a point is a circle with centre at the fixed point and radius is the fixed distance. In this question, some students can make a mistake while applying the distance formula using a line because they leave $x=4$ as it is and apply the distance formula. It is wrong because the general expression has the R.H.S as zero. So, we should be careful while applying the formula and check whether the R.H.S is made to zero or not.