Question

The diameter of a garden roller is 1.4 meter and it is 2 meter long. How much area will it cover in 50 revolutions?

Answer 1

Before solving this question, we must know the formula to find the area of the circle.
The formula to find the circumference of the circle - \[2\pi r\]
CIRCUMFERENCE: The circumference is the perimeter of a circle. That means that circumference of a circle is the length of the boundary of the circle.
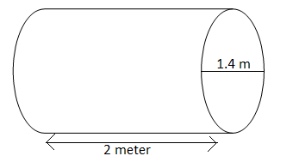
Here is a rough figure of the roller.

Complete step-by-step answer:
The diameter of the roller = 1.4 meter
Radius of the roller = \[\dfrac{d}{2}=\text{ }\dfrac{1.4}{2}\text{ }=\text{ }0.7m\]
Length of the roller = 2 meter

Area covered by the roller in one revolution \[\begin{array}{*{35}{l}}
   =2\pi rh=2\times \dfrac{22}{7}\times radius\times height \\
   ~=2\times \dfrac{22}{7}\times 0.7\times 2 \\
\end{array}\]
Area covered by the roller in 5 revolutions
\[\begin{array}{*{35}{l}}
   =5\times 2\times \dfrac{22}{7}\times 0.7\times 2 \\
   =10\times 0.7\times \dfrac{22}{7}\times 2 \\
   =7\times \dfrac{22}{7}\times 2 \\
   \begin{align}
  & =22\times 2\text{ } \\
 & =\text{ }44 \\
\end{align} \\
\end{array}\]
Therefore, the area covered by the roller in 5 revolutions is 44 square meter, i.e. \[44\text{ }{{m}^{2}}\] .

NOTE:-
The student must do the calculations very carefully. Any mistake in the calculations can make the answer wrong. Also, one must remember the formula to obtain the areas of different polygons as they can come in handy.