Question

The dimensions of a cinema hall are 100m, 60m and 15m. How many persons can sit in the hall, if each requires $150{{m}^{3}}$ of air?

Answer 1

Hint: First of all, we will find the total volume of the cinema hall having dimensions 100m, 60m and 15m. These dimensions represent length, breadth and height of the cinema hall and as this hall is in the form of the cuboid so we know that volume of the cuboid is equal to $l\times b\times h$ where $l,b\And h$ represents length, breadth and height of the cuboid. The number of persons which can be accommodated in the hall is the division of total volume of the hall by $150{{m}^{3}}$.

Complete step-by-step solution:
The dimensions of the cinema hall are given as:
100m, 60m and 15m
The above dimensions are the length, breadth and height of the cinema hall. We know that cinema hall is in the shape of a cuboid and volume of the cuboid is equal to:
$l\times b\times h$
In the above expression, $l,b\And h$ represents length, breadth and height of the cuboid.
In the below figure, we have shown the figure of the hall which is in the form of a cuboid having length, breadth and height as l, b and h respectively.

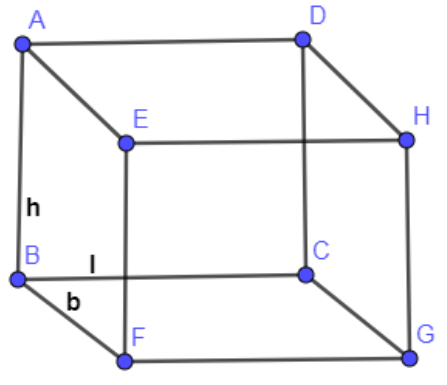
Now, substituting $l=100m,b=60m\And h=15m$ in the above formula of the volume of the cuboid we get,
$\begin{align}
  & \Rightarrow l\times b\times h \\
 & =100m\times 60m\times 15m \\
 & =90000{{m}^{3}} \\
\end{align}$
From the above, we got the volume of the cinema hall as $90000{{m}^{3}}$.
It is given that each person requires $150{{m}^{3}}$ of air so the number of persons which can accommodate in the cinema hall is calculated by dividing the volume of the cinema hall by the volume required by one person.
$\Rightarrow \dfrac{90000}{150}$
One zero will be cancelled out from the numerator and the denominator and we get,
$\begin{align}
  & \Rightarrow \dfrac{9000}{15} \\
 & =600 \\
\end{align}$
Hence, 600 people can sit in the cinema hall.

Note: The mistake that could be possible in the above problem is not writing the units of volume so make sure you have properly written the units of the volume in the above problem. Also, in this problem you are lucky that all the units of length, breadth and height are same (i.e. in metres) and the unit of the volume require by one person is also (in ${{m}^{3}}$) but this is not always the case. You might find some problems where units are not the same so in those cases first make the units same everywhere and then proceed.