Question

The dipole moment of chlorobenzene is 1.5D. Calculate dipole moment of 1,2,3,5-tetrachlorobenzene:
(A) 2.86 D
(B) 2.25 D
(C) 1.5 D
(D) 0 D

Answer 1

Hint: Polar molecules have two poles: positive and negative charged. The product of the magnitude of positive or the negative charge and the distance between the charges is known as the dipole moment ‘D’. For a polyatomic molecule with more than one polar bonds the resultant dipole moment is equal to the:
${{\mu }_{1}}^{2}+{{\mu }_{2}}^{2}+2{{\mu }_{1}}{{\mu }_{2}}\cos \theta $
Where, ${{\mu }_{1}}$ is the dipole moment of one polar bond,${{\mu }_{2}}$ is the dipole moment of other polar bond and the $\text{ }\theta \text{ }$ is the bond between the polar bonds.

Complete Solution :
We have been provided that the dipole moment of chlorobenzene is 1.5D,
We know that the dipole moment is the product of the magnitude of the charge and the distance between the centres of the positive and negative charges. It is denoted by the Greek letter ‘$\mu $'. It is measured in Debye units denoted by 'D'. $1D=3.33564\times {{10}^{-30}} Cm$, where C is Coulomb and m denotes a meter.
We need to find out the dipole moment of 1,2,3,5-tetrachlorobenzene,
1,2,3,5-tetrachlorobenzene is a tetra chlorobenzene carrying chloro groups at positions 1, 2, 3 and 5.

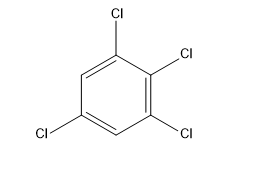
Now, as we need to find its dipole moment So, for that:
We know the angle between 1 and 3 carbon is ${{120}^{\circ }}$,
So, we can say that: $\theta = {{120}^{\circ }}$,
The dipole moment of 2Cl and 5Cl is due to the dipole moment of 1Cl and 3Cl,

So, for determining dipole moment we will be using the formula: ${{\mu }_{1}}^{2}+{{\mu }_{2}}^{2}+2{{\mu }_{1}}{{\mu }_{2}}\cos \theta $,
Where ${{\mu }_{1}}$ and ${{\mu }_{2}}$ is equal to 1.5D and $\theta ={{120}^{\circ }}$,
As we have been given the dipole moment of chlorobenzene: 1.5D,
Now, keeping these values in the formula: ${{\mu }_{1}}^{2}+{{\mu }_{2}}^{2}+2{{\mu }_{1}}{{\mu }_{2}}\cos \theta $,
The dipole moment would be: ${{\left( 1.2 \right)}^{2}}+{{\left( 1.5 \right)}^{2}}+2\times 1.5\times 1.5\cos {{120}^{\circ }}$,
We know the value of: $\cos {{120}^{\circ }} = -\dfrac{1}{2}$,
So, the dipole moment of 1,2,3,5-tetrachlorobenzene comes out to be: $\mu =1.5D$,
So, the correct answer is “Option C”.

Note: The dipole moment depends on the charge at the end of the dipole and its distance from the charge at the other end of the dipole. A dipole moment of zero indicates that there is no partial charge on either end of a covalent bond. The dipoles of the same magnitude and in opposite directions cancel out.