
The direction of angular velocity is along:
A. the tangent to the circular path
B. the inward radius
C. the outward radius
D. the axis of rotation
Answer
503.7k+ views
Hint: The angular velocity of a body only present during the circular motion of a body. For a body with tangential velocity
Complete step by step answer:
Let’s make a diagram of a body executing a circular motion.
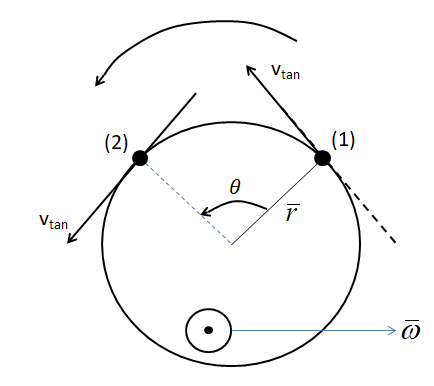
Since, the motion is circular in nature, the circular path followed by the body will have a centre or axis of the path followed. The distance from the axis of the path till the body will be the radius of the circular path, given by (r). The vector form will be:
Now a tangent is drawn to the circular path. The velocity of the body along the direction of the tangent is known as the tangential velocity of the body, given by:
Initially, the body was at position (1) and then, later on it reached a position (2). Since the particle is executing circular motion, the distance from the axis will still remain (r) and the magnitude of the tangential velocity will also remain constant. However, the direction of the tangential velocity will change. The angular displacement caused is given by
As per circular motion, the angular velocity term is given by the rate of change of the angular displacement. That is:
The particle is travelling in anticlockwise direction, when travelling from position (1) to position (2). Hence, using the right hand thumb rule, if we consider curling our fingers along the anticlockwise direction then, the direction of thumb will give us the direction of angular velocity.
Hence, in this case, the direction of angular velocity is outside the plane of the direction of motion given by the axis of rotation of the body.
Hence, the correct answer is option D.
Note:
The relation between the angular velocity
Complete step by step answer:
Let’s make a diagram of a body executing a circular motion.

Since, the motion is circular in nature, the circular path followed by the body will have a centre or axis of the path followed. The distance from the axis of the path till the body will be the radius of the circular path, given by (r). The vector form will be:
Now a tangent is drawn to the circular path. The velocity of the body along the direction of the tangent is known as the tangential velocity of the body, given by:
Initially, the body was at position (1) and then, later on it reached a position (2). Since the particle is executing circular motion, the distance from the axis will still remain (r) and the magnitude of the tangential velocity will also remain constant. However, the direction of the tangential velocity will change. The angular displacement caused is given by
As per circular motion, the angular velocity term is given by the rate of change of the angular displacement. That is:
The particle is travelling in anticlockwise direction, when travelling from position (1) to position (2). Hence, using the right hand thumb rule, if we consider curling our fingers along the anticlockwise direction then, the direction of thumb will give us the direction of angular velocity.
Hence, in this case, the direction of angular velocity is outside the plane of the direction of motion given by the axis of rotation of the body.
Hence, the correct answer is option D.
Note:
The relation between the angular velocity
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




