Questions & Answers
Question
AnswersThe distance between the tops of two trees 20m and 28m high is 17m. The horizontal distance between the two tree is
$(a)$ 11m
$(b)$ 31m
$(c)$ 15m
$(d)$ 9m
Answer
Verified157.8k+ views
Hint - In this type of problem, they usually make right angled triangles and we can use the Pythagoras theorem to solve.
Given that
AB = 20m
AE = 17m
CE = 28m
$\because $ CE = AB + DE
$\therefore $ DE = 8m
With the given data, diagram can be drawn like this
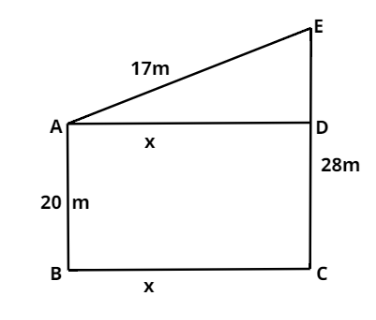
Now we apply the Pythagoras theorem in the ADE triangle.
Then
${\text{A}}{{\text{E}}^2} = {\text{A}}{{\text{D}}^2} + {\text{D}}{{\text{E}}^2}$
${17^2} = {{\text{x}}^2} + {8^2}$
${{\text{x}}^2} = 289 - 64$
${{\text{x}}^2} = 225$
${\text{x = }} \pm {\text{15}}$
$\because $ distance never be negative then
X = 15m
Therefore, the horizontal distance between the two trees is 15m.
Note - In this problem, first let assume the variable for unknown and then apply the Pythagoras theorem and get the value of unknown which is the horizontal distance between the two trees.
Given that
AB = 20m
AE = 17m
CE = 28m
$\because $ CE = AB + DE
$\therefore $ DE = 8m
With the given data, diagram can be drawn like this
Now we apply the Pythagoras theorem in the ADE triangle.
Then
${\text{A}}{{\text{E}}^2} = {\text{A}}{{\text{D}}^2} + {\text{D}}{{\text{E}}^2}$
${17^2} = {{\text{x}}^2} + {8^2}$
${{\text{x}}^2} = 289 - 64$
${{\text{x}}^2} = 225$
${\text{x = }} \pm {\text{15}}$
$\because $ distance never be negative then
X = 15m
Therefore, the horizontal distance between the two trees is 15m.
Note - In this problem, first let assume the variable for unknown and then apply the Pythagoras theorem and get the value of unknown which is the horizontal distance between the two trees.