Question

The earth follows an elliptical orbit around the sun. The ellipse formed by the orbit has a semi-major axis diameter of 150 million kilometers and eccentricity is $\dfrac 1{60}$. Find the difference between the maximum and minimum distance between the earth and the sun.

Answer 1

Hint: It is given that the earth follows an elliptical path around the sun. So, first we will draw an ellipse and since the earth orbits around the sun, we will consider that sun is at one of the foci, say point A. Now to either ends of the ellipse, we can mark points B and C. We have to find maximum and minimum distance, i.e AB and AC and then its difference. We know the maximum distance between the focus and the boundary of the ellipse which is a(1+e) and the minimum distance is a(1-e). We have the values of the semi-major axis, i.e. a and also the eccentricity i.e. e given in the question. With this data, we can solve the question further.

Complete step-by-step answer:
The question gives us the data that the earth is following an elliptical orbit around the sun. It means that there is an orbit in the shape of an ellipse. The sun is therefore supposed to be a one of the foci of the elliptical orbit.
So, we will construct an eclipse with the sun at one of the foci A of the ellipse. The path of the earth is such that it is closest at point B and the furthest at point C. The sun is at one of the foci of the ellipse. So the distance between the sun and the earth is not the same as in a circle.

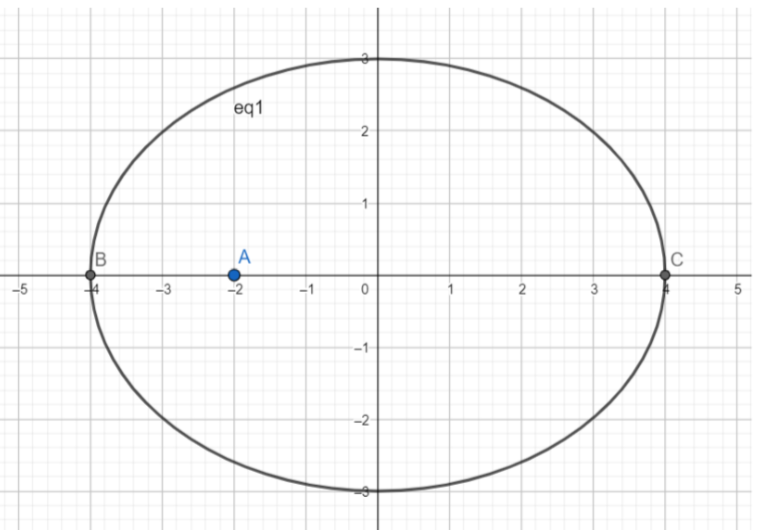
We will first find the maximum distance between the focus and the boundary of the ellipse which is a(1+e). Then we will find the minimum distance which is a(1- e) where a is the diameter of the semi-major axis and e is the eccentricity of the ellipse.
The sun is at one of the foci, at point A. The shortest distance between earth and the sun is AB and the longest is AC.
Now we have been given the semi-major axis diameter, which is a, is-
a = 150 million km
We also know that the eccentricity e = $\dfrac 1{60}$.
The difference between maximum and minimum distance is = a(1+e) - a(1-e)
= 2ae
$=2\times 150\times\dfrac 1{60}$
= 5 million km
This is the required answer.

Note: One should have knowledge about ellipse and its eccentricity to solve this problem. We can also derive the formula for maximum and minimum distance but it is quite lengthy. So, it is better to remember formulas to solve the problem by a shorter method. The formula is easy to memorise, the distance will be the product of a and e. For maximum distance, we take it as a(1+e) and it shows addition of 1 to e. Now, for minimum distance, we take it as a(1-e) and it shows e being subtracted from 1.