Question

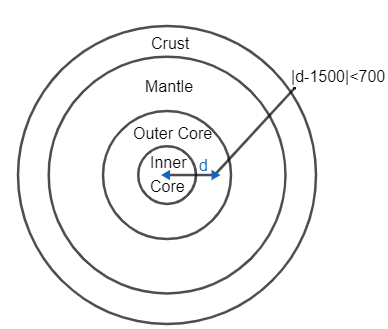
The Earth is made up of four primary layers: the inner core, outer core, mantle, and crust. The distance between the Earth’s center and the outer core is more than 800 miles but less than 2200 miles. Determine which of the following inequalities represents all possible distances, d, in miles, from the Earth’s center that are in the outer core.
A.. \[\left| d+800 \right|<2200\]
B.. \[\left| d-800 \right|<2200\]
C.. \[\left| d+1500 \right|<700\]
D.. \[\left| d-1500 \right|<700\]

Answer 1

Hint: In this question we are given with the extreme values of distance from the centre of Earth to the outer core of the Earth which is the starting point of the outer core which is 800 miles from the centre of Earth and the ending point of the outer core which is 2200 miles from the centre of Earth, and we have to form an inequality which represents all distances in this outer core region from the centre of Earth and we are going to use the formula of inequalities which is \[-a
Complete step by step answer:

In this question we are given with the extreme values of the distance of outer core from the centre of the Earth, the starting point of the outer core or the ending point of the inner core is given at the distance of 800 miles from the centre of the Earth and the ending point of the outer core or the starting point of the mantle is given at the distance of 2200 miles from the centre of the Earth.
We are going to solve the question by making sub-inequalities and then we will form final equality at the end, so the first sub-inequality is,
As it is given in the question that the starting point of the outer core is at a distance of 800 miles from the centre of the Earth,
\[800Also as it is given in the question that the ending point of the outer core is at a distance of 2200 miles from the centre of the Earth,
\[d<2200\]
As both the sub-inequalities can be combined without any obligation, so we get,
\[800Now we have to apply the formula of inequalities which is \[-aBut it can only be applied when both the values before and after the centre variable term are same and in case of our inequality they are different, so we have to make them same by using the following method,
We have to make two equations such that we have to find the number which is when subtracted from the low end as well as from the high end of the inequality gives the same number in value but with opposite sign.
So, the equations are,
\[800-x=-k\]
\[2200-x=k\]
Multiplying the first equation by -1, so that the third term which is on the R.H.S. of the equal to sign.
\[-800+x=k\]
Now we have to find the value of \[x\] by equating both the equations because their third term on R.H.S. of equal to is same, so we get,
\[-800+x=2200-x\]
\[\begin{align}
  & 2x=2200+800 \\
 & 2x=3000 \\
\end{align}\]
\[x=\dfrac{3000}{2}\]
\[x=1500\]
Hence we have to subtract 1500 from the low end of the inequality and add 1500 at the high end of the inequality, so we get,
\[800Subtracting 1500 from the inequality, we get,
\[800-1500\[-700Hence now applying the transformation formula to this inequality, we get, \[-a\[-700Hence the correct option is,
Option. D. \[\left| d-1500 \right|<700\]

Note:
Now why the transformation formula works with the modulus function, it works because modulus function has two outputs that is it can turn \[\left| x \right|=\begin{matrix}
   -x,\left( x<0 \right) \\
   x,\left( x>0 \right) \\
\end{matrix}\] and so we can modify our inequality and just mention either low side of the inequality or the high side of the inequality along with the centre variable term. We can also take the mean of both the high side and the low side of the inequality and then subtract from the whole inequality to form the transformation formula this is a short cut method, now if both the low side and the high side terms of the inequality are negative then we have to add instead of subtracting the mean of both the terms from the whole inequality.